P P: Układ równań x² + y² = 16 x + 4y = 2

vitek1980: rozwiązać, czy zbadać ile ma rozwiązań?

P: najlepiej rozwiązać. Próbowałam ale nie wychodziło. Z góry dziękuję. /

vitek1980: z drugiego równania x=2−4y i podst. do 1.równ (2−4y)²+y²=16 4−16y+16y²+y²−16=0 17y²−16y−12=0 Δ=...

P: tak i delta wynosi 1072

vitek1980: oblicz y₁ i y₂ − normalne równanie kwadratowe

P: właśnie nie wiem co z tym dalej zrobić.

vitek1980:

	−b−√Δ
y1 =
	2a

	−b+√Δ
y2 =
	2a

potem podst. oba policzone "y" do drugiego i obl. x1, x2

P: dobrze, to wiem i tak robiłam w y₁ wychodzi ^{16 − 4√67}₃₄ tak ma być ?

P: nie wiem, nie zrobię tego

vitek1980: dobrze jest tylko skróć przez 2 i potem oblicz x1 i x2 podstawiając obliczone y

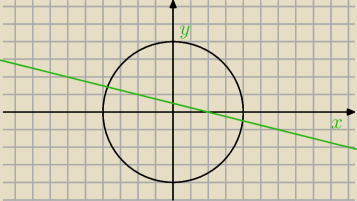
Mila: 1) Rysunek pomocniczy i widzę, że są dwa rozwiązania. x=2−4y (2−4y)²+y²=16 4−16y+16y²+y²=16 17y²−16y−12=0 Δ=1072=16*67

	16−4√67		8−2√67		8+2√67
y1=		=		lub y=
	2*17		17		17

	8−2√67		8+2√67
x1=2−4*		lub x2=2−4*
	17		17

	34−32+8√67		34−32−8√67
x1=		lub x2=
	17		17

	2+8√67		2−8√67
X1=		lub X1=
	17		17