brak pomysłu Abdul: 9.55. Oblicz pole trójkąta, w którym dwie środkowe mają długości 12 cm i 21 cm i przecinają się pod kątem 45°. wynik 84√2 cm²

Eta: Pomagam rysuję .........

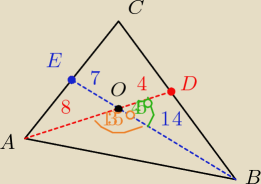
Eta: Witam 1/ środkowe trójkąta dzielą się w stosunku 2:1 licząc od wierzchołka 2/ środkowe dzielą trójkąt ABC na dwa trójkąty o równych polach zatem: IODI= ¹₃ *IADI = ¹₃*12 = 4 to: IADI = 8 podobnie: IOBI= 14 i IOEI= 7 P_Δ ABC = 2*P_ΔADB , i P_ΔADB= P_ΔABO + P_ΔBOD policz : P_ΔBOD =¹₂ IOBI * IODI*sin45^o i P_ΔABO = ¹₂*IBOI*IAOI* sin135^o sin 135^o = sin(180^o − 45^o) = sin45^o Policz , to już proste , powodzenia!

Eta: i jak ? policzyłeś już?

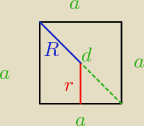Abdul: {Wyszło Dzięki i w nagrodę za wykonaną pracę dokładam gratis zadanie 9.65. Różnica długości promienia okręgu opisanego na kwadracie i promienia wpisanego w kwadrat wynosi 2 cm. Oblicz pole tego kwadratu. wynik 16(3+2√2) cm²

	a		a√2
r=		d=
	2		2

	a		a√2
R=		+ 2=		+ 2
	2		2

R−r=2

Eta: He,he, dla kogo ta "nagroda"? zatem tak:

	a√2		a
R=		i r =
	2		2

R− r =2

	a√2		a
to :		−		= 2 /*2
	2		2

	4
a√2 − a = 4 => a(√2 −1)=4 => a =
	√2 −1

po usunięciu niewymierności otrzymasz: a = 4( √2 +1) to P= a² ...... podstawi i policz ... i po bólu

Abdul: mi wyszło 16 później a=√2 i jeszcze, że P=2a² − 4a√2 + 16

tim: Eto?... Żyjesz? Ukrywasz się?

Eta: A mnie wyszło P= a² = 16*( √2 +1)² = 16( 2 +2√2 +1) = 16( 3+2√2) cm²

Eta: Żyję Timuś ,żyję

Abdul:

	4(√2−1)
Chyba a=		?
	3

Eta: niestety ale źle

	4		4(√2+1)		4(√2+1)
a =		=		=		=4(√2+1)
	√2−1		(√2 −1)( √2+1)		2 −1

Eta: Czy teraz już wiesz , gdzie popełniłeś błąd ? "szejku arabski" ?

Abdul:

	4		4		√2−1		4(√2−1)
a=		=		*		=
	√2−1		√2−1		√2−1		2+1

Abdul: a dlaczego masz √2+1 jak było − 1

tim: Abdul wymnóż (√2 − 1)(√2 − 1) ... A następnie: (√2 − 1)(√2 + 1) = ...

tim: Eto... Możemy na "słówko"? ^^

Eta: od kiedy to? (√2 −1)( √2 −1) = 3 ( √2−1)(√2−1) = ( √2−1)² = 3 −2√2 jasne? więc należy tak usunąć niewymierność: ze wzoru ( a − b) (a +b) = a² − b² więc mnożymy licznik i mianownik przez (√2 +1) zatem mianownik: ( √2 −1)( √2+ 1) = (√2)² −1² = 2 −1 = 1

Abdul: przeczytałem 1134 i teraz wiem że to się mnoży z przeciwnym znakiem czyli z +1 a nie −1 a byłem pewien że to potrafię

Abdul: Eta pls nie bij mnie

Eta: No,........ bo już zwątpiłam w Ciebie

Abdul:

Eta:

Abdul: wyszło mi prawidłowo Ojczyzna jest z was dumna obywatelko

Eta: he,he Rób wszystko , by kiedyś ktoś o Tobie napisał podobnie Powodzenia!