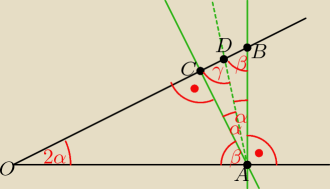
wskazówka: kąt OAC jest równy kątowi OBA KretXXX: Dany jest kąt ostry o wierzchołku O i punkt A leżący na ramieniu tego kąta, A nie równa się O. Przez punkt A poprowadzono dwie proste: prostą k prostopadłą do ramienia OA, Która przecięła drugie ramię kąta w punkcie B, oraz prostą m, prostopadłą do drugiego ramienia, która przecięła to ramię w punkcie C. Dwusieczna kąta ostrego BAC przecięła odcinek BC w punkcie D. wykaż, że |OA| = |OD|

Bogdan: β = 90^o − 2α i β + α = 90^o − 2α + α = 90^o − α = |∡OAD| W trójkącie OAD: 2α + (β + α) + γ = 180^o ⇒ 2α + 90^o − 2α + α + γ = 180^o ⇒ γ = 90⁰ − α = |∡ODA| |∡OAD| = |∡ODA| ⇒ |OA| = |OD| (trójkąt OAD jest równoramienny)