przystawanie trójkątów
Mitchie: W trójkącie równobocznym o boku a przedłużono bok AC poza punkt A o odcinek [AA1].[AA1]=1, bok
AB poza punkt B o odcinek [BB1]. [BB1]=1, bok BC poza punkt C o odcinek CC1, [CC1]=1.
udowodnij, że trójkąt A1B1C1 jest równoboczny.
10 mar 21:52
Beti:
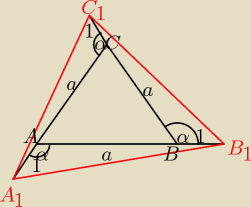
może tak:
|AA
1| = |BB
1| = |CC
1| = 1
|∡A
1AB
1| = |∡B
1BC
1| = |∡C
1CA
1|
|AB
1| = |BC
1| = |CA
1| = a+1
więc na podstawie cechy BKB trójkąty: A
1B
1A, B
1C
1B i C
1A
1C są przystające,
co oznacza, że:
|A
1B
1| = |B
1C
1| = |C
1A
1|
czyli trójkąt A
1B
1C
1 jest równoboczny
cbdu
10 mar 23:30
 może tak:
|AA1| = |BB1| = |CC1| = 1
|∡A1AB1| = |∡B1BC1| = |∡C1CA1|
|AB1| = |BC1| = |CA1| = a+1
więc na podstawie cechy BKB trójkąty: A1B1A, B1C1B i C1A1C są przystające,
co oznacza, że:
|A1B1| = |B1C1| = |C1A1|
czyli trójkąt A1B1C1 jest równoboczny
cbdu
może tak:
|AA1| = |BB1| = |CC1| = 1
|∡A1AB1| = |∡B1BC1| = |∡C1CA1|
|AB1| = |BC1| = |CA1| = a+1
więc na podstawie cechy BKB trójkąty: A1B1A, B1C1B i C1A1C są przystające,
co oznacza, że:
|A1B1| = |B1C1| = |C1A1|
czyli trójkąt A1B1C1 jest równoboczny
cbdu