wartosci fabia: dla jakich wartosci parametru m rownanie ma dokladnie jeden pierwiastek? znajdz ten pierwiastek a) x²−mx+2=0 b)(m−1)x²−2(m+1)x+m−2=0

roxi: prosze o pomoc

bezendu: a kiedy funkcja kwadratowa ma jeden pierwiastek ?

Jolanta: jeden pierwiastek jest wtedy .gdy Δ=0 Δ=0 Δ=m²−8 m²−8=0 dokończ

roxi: jolanta bardzo prosze o rozwiazanie

bezendu: m²=8 m=2√2 lub m=−2√2

Licealista: m²=8 / √ ...

Jolanta: chętnie pomoge ,alew gotowiec nic Ci nie da umiesz to rozwiazac x−3=0

dero2005: m² − 8 = 0 m² = 8 m = √8 = 2√2 lub −2√2

dero2005: b) (m−1)x² − 2(m+1)x + m− 2 = 0 a = m−1 b = −2(m+1) = −2m − 2 c = m −2 Δ = b² − 4*a*c = (−2m−2)² − 4(m−1)(m−2) = 4m² + 8m + 4 − 4(m² − 2m − m +2) = = 4m² +8m + 4 − 4m² +12 m − 8 = 20m − 4 = 0

	4		1
m =		=
	20		5

fabia: bardzo bardzo dziekuje czy moge jeszcze napisac zadania do rozwiazania?

dero2005: dla a) m = 2√2 x² − 2√2x + 2 = 0 Δ = b² − 4ac = (−2√2)² − 4 *1 *2 = 8 − 8 = 0

	−b		2√2
x =		=		= √2
	2a		2

m = −2√2 x² + 2√2x + 2 = 0 Δ = b² − 4ac = (2√2)² − 4*1*2 = 8−8 = 0

	−b		−2√2
x =		=		= −√2
	2a		2

dla b) m = ¹₅ (¹₅−1)x² − 2(¹₅ +1)x + ¹₅ − 2 = 0 −⁴₅x² − ¹²₅x − ⁹₅ = 0 |*5 −4x² − 12x − 9 = 0 Δ = b² − 4ac = (−12)² − 4−(−4)*(−9) = 0

	−b		3
x =		= −
	2a		2

Cusack: w b) trzeba pamiętać jeszcze o przypadku liniowym. dla m=1 też mamy jedno rozwiązanie

fabia: dla jakich wartosci m rownanie ma dwa rozne rozwiazania? a)x2−(m+3)x+m24=0 (m−1)x2−2mx+m=0

fabia: dero2005 serdecznie Pani czy Panu dziekuje za ciepłe słowa i wyrozumiałość

fabia: rozwiaz rownania i nierownosci a) 2x²−7x=0 b)(2x−1)²+x=x²−5x c) (x−√3)(x+√3)=2(x+5)²+22 d)x²−2x>0 e)2x²−5x−3<0 f)x²+10x+25mniejszerowne0 g)x²+6x+9>0

dero2005: a) 2x²−7x = 0 x(2x−7) = 0 x = 0 lub 2x − 7 = 2x = 7

	7
x =
	2

b) (2x−1)² + x = x² −5x 4x² − 4x +1 +x − x² + 5x = 0 3x² + 2x + 1 = 0 Δ = b² − 4ac = 2² − 4*3 *1 = 4−12 = −8 brak rozwiązań c) (x−√3)(x+√3) = 2(x + 5)² + 22 x² − (√3)² = 2(x² + 10x + 25) + 22 x² − 3 = 2x² + 20x + 50 + 22 x² − 2x² − 3 − 20x − 50 −22 = 0 −x² − 20x − 75 = 0 Δ = b² − 4ac = (−20)² − 4*(−1)(−75) = 400 − 300 = 100 √Δ = 10

	−b−√Δ		20−10
x1 =		=		= −10
	2a		−1

	−b+√Δ		20+10
x2 =		=		= 30
	2a		−1

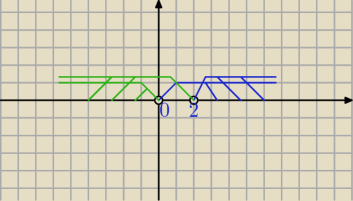
dero2005: d) x² − 2x>0 x(x−2)>0 żeby iloczyn był dodatni czynniki muszą byc albo obydwa dodatnie albo obydwa ujemne x>0 i x−2>0 lub x<0 i x−2 <0 x>0 i x> 2 lub x<0 i x< 2 x>2 lub x<0 x∊(−∞, 0) lub (2, ∞)

roxi: bardzo proszę o rozwiązanie pozostałych przykładów z góry serdecznie dziekuje

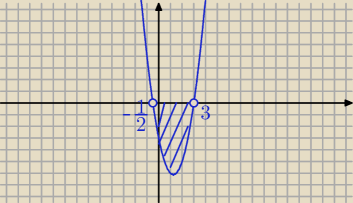
dero2005: e) 2x² − 5x − 3<0 Δ = b² − 4ac = 49 √Δ = 7 x₁ = −¹₂ x₂ = 3 x∊(−¹₂, 3)

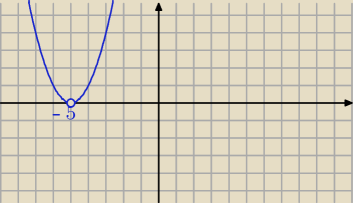
dero2005: f) x² + 10x + 25 ≤0 Δ = b² − 4ac = 10² − 4*1*25 = 100−100 = 0

	−b		−10
x =		=		= −5
	2a		2

x = −5

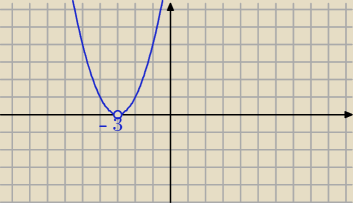
dero2005: g) x² + 6x + 9 >0 Δ = b² − 4ac = 6² − 4*1*9 = 36 − 36 = 0

	−b		−6
x =		=		= −3
	2a		2

x∊(−∞, −3)∪(−3,∞)

roxi: nie wiem jak mogłabym się odwdzięczyć

roxi: dana jest funkcja y=2x+3 podaj wzory obrazow tej funkcji po przekształceniu jej względem osi i poczatku ukladu wspolrzednego

roxi: rozwiaz rownania dwukwadratowe a) x⁴−17x²+16=0 b)x⁴−3(x²−1)=7(x²−3)

bezendu: x⁴−17x²+16=0 x²=t t²−17t+16=0 i teraz policz Δ

bezendu: x⁴−3x²+3=7x²−21 x⁴−3x²+3−7x²+21=0 x⁴−10x²+24=0 x²=t t²−10t+24=0