matura PuRXUTM: Mam prośbę proszę o sprawdzenie wyników z http://www.zadania.info/d1508/76258 1) dla m∊(−2;2) 2 rozwiązania dla m=−2 v m=2 1 rozwiązanie dla m∊(−∞;−2) U (2;+∞) brak rozwiązań

PuRXUTM: 2) to dowód myślę że dobrze udowodniłem, jeżeli a,b∊(0.1) to log_b a >0, log_a b>0 tak ?

	1
3) x∊(−∞;−		>
	5

PuRXUTM:

	π		π		2π		1		1		2
4) x={		,		,		,1		π,1		π,1		π}
	3		2		3		3		2		3

PuRXUTM: 5) dowód, po wielkich trudach doszedłem do 0=0 6) m=√14 v m=−√14

PuRXUTM:

	16		676
7) chyba jedno z najtrudniejszych zadań (x+		)2+(y+4)2=
	3		9

8) Obw=6

zombi: 2) wystarczy podstawienie, że t=log_ba wtedy

	1
4t+		≥4
	t

(2t−1)²≥0

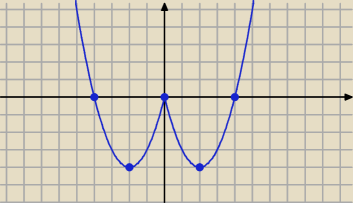
Eta: 1/ za mało tych rozwiązań

PuRXUTM: 9) jak na razie nie umiem zrobić ale jeszcze pomyśle i zajrzę do książek 10) V=5√3 ale coś mi się wydaje że za szybko mi to wyszło jak na zadanie za 6pkt. Jeżeli ktoś ma trochę wolnego czasu albo już to przerobił to proszę o sprawdzenie

PuRXUTM: no właśnie tego Eto nie byłem pewny... tylko jak to rozwiązać algebraicznie...? bo ja sobie podstawiłem za y do pierwszego −m²

zombi: 5) Wcale nie takie trudy: x=pq^a y=pq^b z=pq^c

	pqa		pqb
(		)√c=(		)√a
	pqb		pqc

(q^a−b)^√c=(q^b−c)^√a ⇒ √c(a−b)=(b−c)√a b(√a+√c)=(√a+√c)√ab b=√ac b²=ac <−−− geo, czyli ckd

PuRXUTM: zombi a jak przeszedłeś z 4 linijki od końca do 3 od końca ?

zombi: (q^a−b)^√c − potęgi potęgi czyli mnożymy wykładniki. dalej po obu stronach mam tą samą podstawę czyli przyrównujemy wykłandiki z obu stron, to masz na myśli?

PuRXUTM: jedną linijkę niżej

zombi: √ca−b√c=−c√a+b√a −b√c−b√a=−c√a−a√c −b(√c+√a)=−(c√a+a√c) b(√c+√a)=(√a+√c)√ac

zombi: wszystko z b na jedną

PuRXUTM: dzięki Jak masz ochotę to popatrz jeszcze na resztę zadań, wpadnę jeszcze wieczorem Dzięki wszystkim

zombi: 8) Cosinusem prawda? Ładnie wychodzi. 6) Trzeba sobie rozbroić, ale idzie jakoś. 4) Sobie policze za chwile

zombi: 4) 4sinx sin2x − 3cosx cos2x = 4sin³x sin2x + 3cosx sin2x [ 4(sinx − sin³x) ] = 3cosx [ cos2x + 1 ] sin2x sinx [4(1−sin²x)] = 3cosx [ cos²x − sin²x + cos²x + sin²x] sin2x sinx [4(1−sin²x)] = 3cosx [ 2(1−sin²x) ] sin2x sinx [4(1−sin²x)] = 6cosx ( 1−sin²x ) (1−sin²x)[ 4sinx sin2x − 6cosx ] = 0 (1−sin²x) (2cosx) (4sin²x−3) = 0 raczej coś takiego, o ile się nie walnąłem

PuRXUTM: dzięki zombi za poświęcony czas