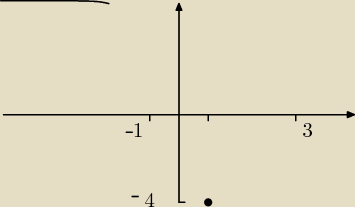
Dana jest funkcja ... FUNKCJA: Dana jest funkcja f(x) = x² + 2x − 3 a) narysuj wykres tej funkcji b) oblicz jej miejsce zerowe c) określ przedziały monotoniczności tej funkcji d) wyznacz największą i najmniejszą wartość tej funkcji w przedziale <1,5> e) dla jakich argumentów funkcja ta przyjmuje wartości dodatnie, a dla jakich ujemne? f(x) = x² + 2x − 3 Δ = b² − 4ac Δ = 4 − 4 x (−3) Δ = 4 + 12 Δ = 16 √Δ = 4

	− 2 − 4
x1 =		= −3
	2

	−2 + 4
x2 =		= 1
	2

A − rysunek ( mz: −1 , 3 ) − nie umiałem tego tak narysować. [ ramiona skierowane ku górze, przechodzi przez pkt −1 i 3 na osi X, wierzchołek ( −1, −4 ). B: x₁ = − 3 x₂ = 1 Mz: ( −1 , 3 ) C. p = − 1 ( na osi OX ) q = − 4 ( na osi OY ) W = ( −1, −4 ) D. nie rozumiem, gdzie jest ten przedział < 1,5 > ? E. f>0 <=> ( − ∞, −1) U ( 3, −∞) f<0 <=> ( −1, 3 ) Czy dobrze? Prosiłbym o pomoc w pkt D i o sprawdzenie zapisu w pkt E. Pozdrawiam.

FUNKCJA: Jednak rysunek mi nie wyszedł.

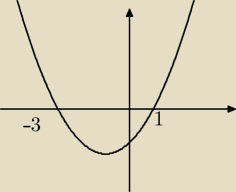ff: A no nie wyszedł B ok, sprawdzasz je podstawiając do f(x): f(1)=0, f(−3)=0, czyli w porządku C też dobrze, (tutaj w ramach szybkiego sprawdzenia: x wierzchołka jest dokładnie pośrodku miejsc zerowych czyli −1) f(−1) = −4 ok D: największa wartość na przedziale <1,5> czyli szukasz największego y (czyli wartości y=f(x)) dla x ∊ <1,5> z rysunku widać, że będzie to f(5) (na przedziale <1,5> f(x) jest rosnąca) E ok

ff: pośpieszyłem się z E: f(x) > 0 ⇔ x ∊ ( − ∞, −3) U ( 1,∞) f(x) < 0 ⇔ x ∊ (−3,1)

ff: co do: Mz (1,−3) − tak tego nie zapisujemy jak już to miejsca zerowe: {−3, 1} (zbiór elementów, nie przedział)