geometria analityczna Imosek: Witam! mam poblem z zadaniem, nie wiem czy dobrze mysle...bo ja bym to rozwiazal tak i i niby wychodzi mi bledna odpowiedz. bo w ksiazce jest calkiem inaczej to pokazane: NArysuj zbior punktow plaszczyzny, ktorych wspolrzedne spelniaja uklad { y=|x|−2 y=−|x+2|} no to ja b ym to zrobil tak ze: 1. |x| = {x, x≥0 −x, x<0} 2. |x+2| = {x+2, x≥−2 −x−2, x<−2} i teraz rozpatrywalbym trzy przypadki: 1. x≥0 x≥−2 { y=x−2 y=−(x+2)=−x−2} 2y=−4 ==> y=−2 dla x≥0 2. x<0 x≥−2 { y=−x−2 y=−(x+2)=−x−2} 0 = 0 uklad tozsamosciowy w przedziale <−2,0) 3. x<0 x<−2 { y=−x−2 y=−(−x−2) = x+2} y=0 dla x∊ (∞,−2) teraz czy tak nie moze byc? jak nie to czemu i co robie zle?

krystek: Musisz podzieloc na przedziały x∊(−∞,−2) x∊<−2,0) x∊<0.∞)

Imosek: no przeciez mam tak podzielone i teraz rysowac tak? to co mi wyszlo? Mozesz narysowac jakby to wygladalo ?

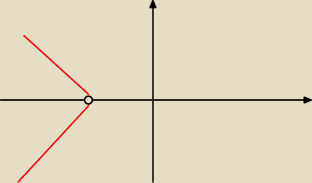
krystek: I przedział wykres tak wygląda y=−x−2 y=x+2

krystek: II y=−x−2 y=−x−2

Imosek: no i dalej?

Imosek: halooo

krystek: Masz III przedział i rozpisz

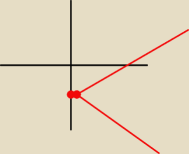
Imosek: to tak i teraz narysowac to wsztko razem i to jest wynik? czy jak czy miejsca tych przeciec?

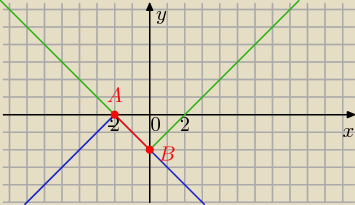
Mila: y=|x|−2 zielony wykres y=−|x+2| niebieski układ równań spełniają współrzędne punktów należących do odcinka AB: x∊<−2,0> i y=−x−2