Sprawdzenie. KevyB: y = −5x + 7 a) Miejsce Zerowe −5x + 7 = 0 −5x = −7 | : −5 x = 1,4 b) Współrzędne przecięcią wykresu z Y y = −5x + 7 y = 7 (1,4 ; 7) c) Wykres Funkcji hmm, to zaraz d) Oblicz Wartość Funkcji dla argumentu równego −6 y = −5*6 + 7 y = −23 e) Znajdź argument dla którego wartość funkcji wynosi −8 −5x + 7 = −8 −5x = −8 − 7 −5x = −15 | : −5 x = 3 f) Oblicz dla jakich argumentów funkcja przyjmuje wartości dodatnie −5x + 7 > 0 −5x > −7 | : −5 x < 1,4 g) Oblicz dla jakich argumentów funkcja przyjmuje wartości mniejsze od −3 −5x + 7 < −3 −5x < −3 − 7 −5x < −10 | : −5 x > 2 h) Określ dla jakich argumentów funkcja przyjmuje wartości ujemne −5x + 7 < 0 −5x < −7 | : −5 x > 1,4 i) Określ dla jakich argumentów funkcja przyjmuje wartości większe od 5 −5x + 7 > 5 −5x > 5 − 7 −5x > −2 | : −5 x < 0,4 j) Określ monotoniczność funkcji Narysuje wykres wpierw k) Sprawdź rachunkowo czy punkty A(−3 ; 1) i B(9 ; −1) należą do wykresu Jak? l) Czy wykres przechodzi przez punkt A(1 ; −7), a funkcja przyjmuje wartość dodatnią dla x>4 To łatwo chyba czy przyjmuje, sprawdzam przeciesz kiedy przyjmuje wartości dodatnie, a jest to tylko dla x < 1,4 no nie? Ale sprawdzić to jak z tym? Dzięki za sprawdzenie, dopomoc ^^

tim: Więc tak. a i d) dobrze. b) Punkt przecięcia nie jest taki. Ogólnie brakuje ładnych odpowiedzi i odpowiedniego dosadnie poprawnego opisu. np. (f(−6))

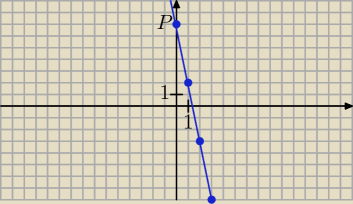
Bogdan: Zapisy Twoje nie są zbyt poprawne. Powinno być tak: y = −5x + 7

	7
a) Miejsce zerowe: y = 0 ⇔ −5x + 7 = 0 ⇒ 5x = 7 ⇒ x =		.
	5

b) Współrzędne przecięcia wykresu z osią y: x = 0 ⇒ y = 7, P(0, 7). c) Wykres funkcji (można narysować bez tabelki). d) Oblicz wartość funkcji dla argumentu równego −6: x = −6 ⇒ y = −5*(−6) + 7 = 37. e) Znajdź argument dla którego wartość funkcji wynosi −8: y = −8 ⇔ −5x + 7 = −8 ⇒ 5x = 15 ⇒ x = 3. f) Oblicz dla jakich argumentów funkcja przyjmuje wartości dodatnie.

	7
y > 0 ⇔ −5x + 7 > 0 ⇒ 5x < 7 ⇒ x <		.
	5

g) Oblicz dla jakich argumentów funkcja przyjmuje wartości mniejsze od −3. y < −3 ⇔ −5x + 7 < −3 ⇒ 5x > 10 ⇒ x > 2. h) Określ dla jakich argumentów funkcja przyjmuje wartości ujemne.

	7
y < 0 ⇔ −5x + 7 < 0 ⇒ 5x > 7 ⇒ x >		.
	5

i) Określ dla jakich argumentów funkcja przyjmuje wartości większe od 5.

	2
y > 5 ⇔ −5x + 7 > 5 ⇒ 5x < 2 ⇒ x <		.
	5

j) Określ monotoniczność funkcji. Funkcja jest malejąca, ponieważ współczynnik kierunkowy prostej a = −5 < 0. k) Sprawdź rachunkowo czy punkty A(−3 ; 1) i B(9 ; −1) należą do wykresu. x = −3 ⇒ y = −5*(−3) + 7 = 22 ≠ 1, punkt A(−3, 1) nie należy do wykresu funkcji. x = 9 ⇒ y = −5*9 + 7 = −38 ≠ −1, punkt B(9, −1) nie należy do wykresu funkcji. l) Czy wykres przechodzi przez punkt C(1 ; −7), a funkcja przyjmuje wartość dodatnią dla x>4? x = 1 ⇒ y = −5*1 + 7 = 2 ≠ −7, punkt C(1, −7) nie należy do wykresu funkcji. Na podstawie punktu f) i h) wiemy, że funkcja przyjmuje wartości dodatnie dla

	7		7
x <		oraz przyjmuje wartości ujemne dla x >		, czyli nie jest dodatnia
	5		5

dla x > 4. Jeszcze uwagi na koniec. Jeśli w zadaniu nie ma wyraźnego polecenia o zapisywaniu wyników w postaci liczb dziesiętnych, to nie zamieniamy ułamków na liczby dziesiętne. Nie można w tym samym zadaniu stosować tych samych oznaczeń dla różnych parametrów zadania. W Twoich zapisach występuje punkt A dwukrotnie z różnymi współrzędnymi.

KevyB: Tak tylko ze jakbym wlasnie chcial bez postaci dziesietnych np zaznaczyc taką współrzędną to musiałbym jedną kratke dzielić na 5 części a na takiej małej kartce to nie byłoby zbyt wiele miejsca żeby tak robić i strasznie napaćkane by było szczególnie że ja ją znam, i woli żebyśmy tak pisali. A tamte pozostałe to przestudiuje i zaczaje

Bogdan:

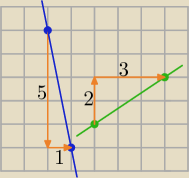
	−5
y = −5x + 7 ⇒ y =		x + 7
	1

Zaznaczasz na osi y punkt o wartości 7, potem opuszczasz się o 5 jednostek w dół i 1 jednostkę

	−5
w prawo (bo jest pochylenie równe		).
	+1

	2
Gdyby równanie prostej było: y =		x − 4, to zaznaczasz na osi y punkt −4, potem
	3

	+2
od tego punktu przesuwasz się w górę o 2 i dalej w prawo o 3 (bo jest pochylenie		).
	+3

edyta: proszę o pomoc w rozwiązaniu i wytłumaczenie 1) Dana jest funkcja określona wzorem :f(x)=( 2x −3)² +(x−4)²−4x²+10x−16. a) doprowadź do najprostszej postaci wzór tej funkcji, wykonując działania i redukując wyrazy podobne , b) narysuj wykres tej funkcji i podaj jej zbiór wartości , c) wyznacz maksymalny przedział, w którym wartości funkcji są ujemne, d) wyznacz maksymalny przedział, w którym funkcja jest malejąca, e) narysuj wykres funkcji g(x)=f(−x) 2) Największa wartość funkcji kwadratowej f jest równa 9. Liczby 0 i 6 są miejscami zerowymi tej funkcji . Wyznacz wzór funkcji f i zapisz go w postaci ogólnej . Bardzo pilne proszeeeeeee