wyznacz y jako funkcje x i naszkicuj wykres tej funkcji. maturalny:

	1		1
z równania		+		=1 wyznacz y jako funkcje x i naszkicuj wykres tej funkcji.
	y−1		x+1

maturalny: założenia y≠1 i x≠−1 prawa strona do wspolnego mianownika z lewą I tutaj kończą się moje pomysły po karkołomnych przekształceniach wyszło mi x²(2y−2−y²+y)+x(4y−y²−1)+y−1=0 ale co dalej? z góry dziękuje za odp.

maturalny: dwie delty?

maturalny: czy 2y−2−y²+y=0 i 4y−y²−1=0 i y−1=0 wtedy i tylko wtedy całośc równa 0?

aw:

	1
y=		+ 2
	x

Dres: Może lepiej nie komplikować sobie życia i wrzucać do wspólnego mianownika zarówno y jak i x? Zostaw y po jednej stronie i przekształcaj dalej po drugiej!

ICSP:

1		1
	= 1 −
y−1		x−1

1		x−1 − 1
	=
y−1		x−1

	x−2
y−1 =
	x−1

	x−2
y =		+ 1
	x−1

	1
y =		+2
	x−2

maturalny: nierozumiem przejścia z drugiej linijki do trzeciej dlaczego nagle z mianownika y−1 przeszlo do licznika, w ogole nie pomnozone z proporcji ani nie przeksztalcone w zaden sposob

ICSP: Bo mi się nie przewróciło. Poprawna trzeci linijka to :

	x−1
y − 1 =
	x−2

zatem czwarta :

	x−1
y =		+ 1
	x−2

dalej już dobrze

maturalny: ok. dzieki, ale jesli chodzi o sprowadzanie do wszystkiego do wspolnego mianownika lub dzialanie szybszym przeksztalceniem jak wyzej, to zastanawia mnie to kiedy która strategia dziala lepiej i od czego to zalezy? macie jakies wskazówki?

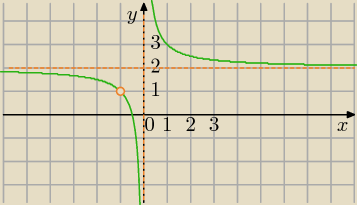
Mila: To najszybszy sposób, alle ICSP zrobił literówkę w mianowniku

1		1
	+		=1 y≠1 i x≠−1
y−1		x+1

1		1
	=1−
y−1		x+1

1		x+1−1
	=
y−1		x+1

1		x
	=
y−1		x+1

	x+1
y−1=
	x

	1
y−1=1+
	x

	1
y=		+2 i x≠0
	x

maturalny: dzięki bardzo. moja watpliwość tyczy się tylko tego w jakich przypadkach w ten sposob a kiedy sprowadzajac wszystkie liczby do wspolnego mianownika? czy ja powinienem byc tak wycwiczony zeby od razu to zauwazyc czy zwyczajnie metoda prob i bledow szukac rozwiazania?