Matura próbna. Bogdan: Matura próbna − poziom podstawowy. Dzień dobry. Zamieszczam próbny zestaw maturalny. Proszę przez najbliższe 4 dni nie zamieszczać tu rozwiązań zadań. Każdy, kto chce być oceniony może wysłać rozwiązania na adres matura@vp.pl Sprawdzę nadesłane rozwiązania, ocenię, skomentuję i odeślę na podany przez autora rozwiązań adres. Wolałbym zobaczyć rozwiązania pisane odręcznie, a nie na komputerze, ponieważ ocenie podlegać będzie również forma i czytelność zapisów i ewentualnych rysunków. Można więc napisać rozwiązania, zeskanować je lub sfotografować i przesłać w postaci plików graficznych. Zadania. 1. (4 pkt). Ile liczb naturalnych jest rozwiązaniem nierówności: (x + 2²⁰⁰⁹)² − (x − 2²⁰⁰⁹)² < 2²⁰¹⁷ 2. (6 pkt). Pole powierzchni bocznej stożka wynosi 8, a pole powierzchni całkowitej 12. Znajdź miarę kąta nachylenia tworzącej stożka do płaszczyzny podstawy.

	√3 + √2		√3 − √2
3. (6 pkt). Dane są liczby: a =		+
	√3 − √2		√3 + √2

i b = NWD(210, 165). a) Wyznacz liczby a, b. b) O ile procent liczba a jest mniejsza od liczby b? 4. (4 pkt). W sklepie z odzieżą cenę pewnej marynarki kosztującej 150 zł obniżono o 20%. Ponieważ tej marynarki nikt nadal nie kupował, ponownie obniżono jej cenę − tym razem o 15%. Podaj cenę marynarki po obu obniżkach. Oblicz, o ile procent w stosunku do ceny pierwotnej cena marynarki po obu przecenach jest niższa.

	4x − 5
5. (4 pkt). Rozwiąż nierówność		≥ x.
	x + 1

6. (8 pkt). Dane są zbiory: A = {x ∊ R: 5x² + 18x − 35 > 0} i B = {x ∊ R: √2x − 2≤ x − √2}. Wyznacz zbiory: A ∪ B, A ∩ B, A \ B, B \ A. 7. (4 pkt). Wyznacz najmniejszą i największą wartość funkcji: f(x) = x² − 2x + 3 w przedziale <−5, 0>. 8. (3 pkt). Zbadaj, czy istnieje taki kąt α, że

	1		√2 − 1
sinα =		i cosα =		.
	√2 + 1		2

9. (6 pkt). Pole koła opisanego na kwadracie jest o 8π większe od pola koła wpisanego w ten kwadrat. Oblicz pole kwadratu.

	3
10. (5 pkt). Dane są liczby:		i 12. Między te liczby wstaw:
	2

	3
a) dwie liczby: a, b tak, aby liczby:		, a, b, 12 tworzyły ciąg arytmetyczny;
	2

	3
b) dwie liczby: c, d tak, aby liczby:		, c, d, 12 tworzyły ciąg geometryczny.
	2

Można korzystać z maturalnych tablic matematycznych i prostego kalkulatora. Proszę nie zamieszczać na forum rozwiązań zadań do dnia poprawkowej matury z matematyki.

Pola: Chciałabym zadań tylko 1 pytanie. Chodzi mi o objaśnienie skrótu w zadaniu 3 przy podpunkcie b, a mianowicie NWD ?

Pola: Właściwie to pytania nie było

Bogdan: Nie udzielam tu do czasu poprawki żadnych wyjaśnień.

andriosza: ahhh

Eta: Witam Wszystkich! Ja już rozwiązałam te zadania ( w czasie 18 min). Myślę,że na max. ilość punktów. No , ale... jako ,że Bogdan jest bardzo skrupulatnym "egzaminatorem" to być może, że ze 2pkt. by mi odliczył , chociażby za nie tak piękne rys. jakie Bogdan nam tu często prezentuje. Pozdrawiam ! , życzę powodzenia PS; Rozwiązania zachowuję narazie tylko dla siebie , przez czas trwania "ciszy" .

Bogdan:

Eta:

olcia: y =2x + 3

Madzia ...: ludki kochane...mam problem i potrzebuje pomocy.... pomoze ktoś?

	1
mam np cos takiego : f(x) =		+1 ? czy ktoś wie jak to wtedy przesunąć
	x −2

Wydi: f(x)=¹_x o 2 jednostki w prawo i 1 jednostkę do góry.

Bogdan: Dobry wieczór, a właściwie dzień dobry. Postanowiłem zakończyć ciszę i podać rozwiązania zadań. Kto chciał rozwiązać, to już rozwiązał. Rozwiązania poszczególnych zadań zamieszczam w kolejnych postach. Najpierw jednak podzielę się refleksjami z wieloletniego sprawdzania prac oraz jakie nasunęły mi się podczas lektury i sprawdzania zadań nadesłanych na adres matura@vp.pl. Egzamin maturalny jest sprawdzianem dojrzałości zdającego, jego wiedzy i umiejętności nabytych podczas kilkunastoletniej nauki w szkole, nie bez powodu jeszcze niedawno nazywano ten egzamin egzaminem dojrzałości. Biorąc pracę do ręki, zapoznając się z jej treścią, czytając rozwiązania, można dość dokładnie scharakteryzować jego autora. Widać, czy jest to osobnik zasługujący na miano człowieka dojrzałego, samodzielnego i gotowego na kolejne życiowe wyzwania, czy też jest to ktoś wyrośnięty, ale wciąż dziecinny, niesamodzielny, niedouczony i ciągle oczekujący na czyjąś pomoc. Można zobaczyć kogoś dbającego o swój wizerunek, ale też zobaczyć można flejtuchów, których praca jest upstrzona bazgrołami, brzydkimi przekreśleniami, rozrzuconymi po całej stronie fragmentami rozwiązań zmuszającymi egzaminatora szukania wzrokiem ciągu dalszego, niestarannymi rysunkami. Dostrzec można osoby rozumiejące treść zadań, jasno, logicznie i zdroworozsądkowo prowadzące swoje rozwiązania, ale także osoby nie wiedzące, o co chodzi, błądzące w rozwiązaniu, prowadzące rozwiązania zawiłą i pokrętną drogą w przeświadczeniu, że wynik końcowy się liczy, trzymające się kurczowo schematu, szablonu, popełniające błędy rachunkowe, nie umiejące w prosty sposób przekształcać wyrażeń, z dużymi brakami wiedzy. Proszę pamiętać, żeby pisać czytelnie, wyraźnie, bez żadnych ozdobników, tak, by egzaminator nie musiał zastanawiać się, co autor miał na myśli. Należy opisywać wprowadzone oznaczenia literowe, nie trzeba przepisywać wzorów z dołączonej do arkusza egzaminacyjnego tablicy wzorów, pomyłki nie wolno zamazywać, należy je delikatnie przekreślić jedną kreską. Szczególną starannością trzeba się wykazać przy sporządzaniu rysunków i ich oznaczeń. Mam nadzieję, że uwagi, jakie tu przekazuję, będą pomocne. W kolejnych postach zamieszczam rozwiązania zadań.

Bogdan: 1. (4 pkt). Ile liczb naturalnych jest rozwiązaniem nierówności: (x + 2²⁰⁰⁹)² − (x − 2²⁰⁰⁹)² < 2²⁰¹⁷ i x ∊ ℕ Rozwiązanie. (x + 2²⁰⁰⁹ − x + 2²⁰⁰⁹)(x + 2²⁰⁰⁹ + x − 2²⁰⁰⁹) < 2²⁰¹⁷ 2*2²⁰⁰⁹*2x < 2²⁰¹⁷ 2²⁰¹¹x < 2²⁰¹⁷ / : 2²⁰¹¹ x < 2⁶ i x ∊ ℕ ⇒ x < 64 i x ∊ ℕ ⇒ x ∊ {0, 1, 2, 3, ... , 62, 63} Odp.: Rozwiązaniem nierówności są 64 liczby naturalne.

Bogdan: 2. (6 pkt). Pole powierzchni bocznej stożka wynosi 8, a pole powierzchni całkowitej 12. Znajdź miarę kąta nachylenia tworzącej stożka do płaszczyzny podstawy. Rozwiązanie. α − miara kąta nachylenia tworzącej stożka do płaszczyzny podstawy, α ∊ (0^o, 90^o), R − długość promienia podstawy stożka, L − długość tworzącej stożka. Pole powierzchni bocznej: P_B = 8 ⇒ πRL = 8, Pole powierzchni całkowitej: P_C = 12 ⇒ πR² + πRL = 12, Pole powierzchni podstawy: P_P = P_C − P_B ⇒ πR² = 12 − 8 = 4 ⇒

	2
⇒ R = √4/π =
	√π

	2		4
πRL = 8 ⇒ π*		*L = 8 ⇒ L =
	√π		√π

	R		2   √π		1
cosα =		=		⇒ cosα =		⇒ α = 60o.
	L		4   √π		2

Odp.: Miara kąta nachylenia tworzącej stożka do płaszczyzny podstawy jest równa 60^o.

Bogdan:

	√3 + √2		√3 − √2
3. (6 pkt). Dane są liczby: a =		+
	√3 − √2		√3 + √2

i b = NWD(210, 165). a) Wyznacz liczby a, b. b) O ile procent liczba a jest mniejsza od liczby b? Rozwiązanie. a)

	√3 + √2		√3 − √2
a =		+		=
	√3 − √2		√3 + √2

	(√3 + √2)2 + √3 − √2)2
=		=
	(√3 − √2)(√3 + √2)

	3 + 2√6 + 2 + 3 − 2√6 + 2
=		= 10
	3 − 2

210 = 2*3*5*7, 165 = 3*5*11, b = NWD(210, 165) = 3*5 = 15. b)

	b − a		15 − 10		1		1
		* 100% =		* 100% =		* 100% = 33		%.
	b		15		3		3

	1
Odp.: a = 10, b = 15, liczba a jest mniejsza od liczby b o 33		%
	3

Bogdan: 4. (4 pkt). W sklepie z odzieżą cenę pewnej marynarki kosztującej 150 zł obniżono o 20%. Ponieważ tej marynarki nikt nadal nie kupował, ponownie obniżono jej cenę − tym razem o 15%. Podaj cenę marynarki po obu obniżkach. Oblicz, o ile procent w stosunku do ceny pierwotnej cena marynarki po obu przecenach jest niższa. Rozwiązanie. Cena marynarki po pierwszej obniżce wynosi 80% poprzedniej ceny, cena marynarki po drugiej obniżce wynosi 85% poprzedniej ceny, cena po dwóch obniżkach = 150 * 0,8 * 0,85 = 102 [zł]

150 − 102		48
	* 100% =		* 2% = 32%.
150		3

Odp.: Cena marynarki po dwóch przecenach wynosi 102 zł i jest niższa o 32% od ceny pierwotnej. Dodatkowe uwagi poza rozwiązaniem. Prawie wszyscy w zadaniach z cenami układają proporcje, co świadczy o niepraktycznym podejściu do zadania. Czy przekupka na targowisku lub sprzedawca w swoim sklepiku osiedlowym chcąc obniżyć lub podwyższyć cenę bawi się w proporcje? Nie, oni wyznaczają nową cenę kilkoma kliknięciami w klawisze kalkulatora stosując metodę pokazaną w tym rozwiązaniu. To jest przecież zadanie z zastosowań matematyki w praktyce.

Bogdan:

	4x − 5
5. (4 pkt). Rozwiąż nierówność		≥ x
	x + 1

Rozwiązanie. Założenie: x ≠ −1.

	4x − 5		4x − 5		4x − 5 − x2 − x
		≥ x ⇒		− x ≥ 0 ⇒		≥ 0 ⇒
	x + 1		x + 1		x + 1

	−x2 + 3x − 5
⇒		≥ 0
	x + 1

Wyznaczam Δ dla trójmianu −x² + 3x − 5, Δ = 9 − 20 < 0, a więc dla każdej wartości x∊R trójmian −x² + 3x − 5 < 0. Skoro wyrażenie w liczniku jest ujemne, to nierówność jest spełniona wtedy, gdy wyrażenie w mianowniku jest też ujemne, czyli x + 1 < 0 ⇒ x < −1.

	4x − 5
Odp.:		≥ x dla x < −1.
	x + 1

Dodatkowe uwagi. Nagminną manierą, która razi, jest zapisywanie wzorów, które znajdują się w dołączonym do arkusza egzaminacyjnego zestawie wzorów oraz powtarzanie oznaczenia literowego w działaniach rachunkowych, np.: Δ = b² − 4ac Δ = 9 − 4*(−1)*(−5) Δ = 9 − 20 Δ = −11 Δ < 0 Lepiej jest tak: Δ = 9 − 4*(−1)*(−5) = 9 − 20 = −11 < 0, a jeszcze lepiej tak: Δ = 9 − 20 < 0 (proste obliczenia rachunkowe typu 4*5 można wykonywać w pamięci).

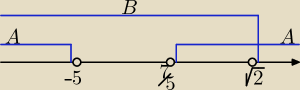
Bogdan: 6. (8 pkt). Dane są zbiory: A = {x ∊ R: 5x² + 18x − 35 > 0} i B = {x ∊ R: √2x − 2 ≤ x − √2}. Wyznacz zbiory: A ∪ B, A ∩ B, A \ B, B \ A. Rozwiązanie. A. 5x² + 18x − 35 > 0, Δ = 324 + 700 = 1024, √Δ = 32,

	−18 − 32		−18 + 32		14		7
x1 =		= −5, x1 =		=		=
	10		10		10		5

+ + + +

	7
−−−−−(−5)−−−−−(75)−−−−−> A: x ∊ (−∞, −5)∪(		, +∞)
	5

− − B. √2x − 2 ≤ x − √2 ⇒ √2x − x ≤ 2 − √2 ⇒ ⇒ (√2 − 1)x ≤ √2(√2 − 1) / : (√2 − 1) x ≤ √2 B: x ∊ (−∞, √2) Odpowiedzi: A∪B = R

	7
A∩B = (−∞, −5)∪(		, √2>
	5

A \ B = (√2, +∞)

	7
B \ A = <−5,		>
	5

Bogdan: 7. (4 pkt). Wyznacz najmniejszą i największą wartość funkcji: f(x) = x² − 2x + 3 w przedziale <−5, 0>. Rozwiązanie. f(x) = x² − 2x + 3 dla x ∊ <−5, 0>

	2
Odcięta wierzchołka paraboli xw =		= 1 ∉ <−5, 0>
	2

f(−5) = 25 + 10 + 3 = 38 f(0) = 3 Odp. Najmniejsza wartośc funkcji jest równa 3, największa 38.

Bogdan: 8. (3 pkt). Zbadaj, czy istnieje taki kąt α, że:

	1		√2 − 1
sinα =		i cosα =		.
	√2 + 1		2

Rozwiązanie:

	1		√2 − 1		√2 − 1
sinα =		*		=		= √2 − 1.
	√2 + 1		√2 − 1		2 − 1

Korzystam z jedynki trygonometrycznej.

	1		5		5
sin2α+cos2α = (√2−1)2 +		(√2−1)2 =		(2−2√2+1) =		(3−2√2) ≠ 1.
	4		4		4

Odp.: Taki kąt nie istnieje.

Bogdan: 9. (6 pkt). Pole koła opisanego na kwadracie jest o 8π większe od pola koła wpisanego w ten kwadrat. Oblicz pole kwadratu. Rozwiązanie. a − długość boku kwadratu,

	a√2
R − długość promienia okręgu opisanego na kwadracie, 2R = a√2 ⇒ R =		,
	2

	a
r − długość promienia okręgu wpisanego w kwadrat, 2r = a ⇒ r =		.
	2

Pole powierzchni kwadratu: P = a²

	2a2		a2		a2
πR2 − πr2 = 8π / : π ⇒		−		= 8 ⇒		= 8 ⇒ a2 = 32
	4		4		4

Odp.: Pole powierzchni kwadratu jest równe 32 [j²].

Bogdan:

	3
10. (5 pkt). Dane są liczby:		i 12. Między te liczby wstaw:
	2

	3
a) dwie liczby: a, b tak, aby liczby:		, a, b, 12 tworzyły ciąg arytmetyczny;
	2

	3
b) dwie liczby: c, d tak, aby liczby:		, c, d, 12 tworzyły ciąg geometryczny.
	2

Rozwiązanie. a) Ciąg arytmetyczny (a_n):

	3
a1 =		,
	2

	3		1		1
a4 = 12 ⇒		+ 3r = 12 / : 3 ⇒		+ r = 4 ⇒ r = 3		,
	2		2		2

	3		1
a2 = a1 + r = a =		+ 3		= 5,
	2		2

	1		1
a3 = a2 + r = b = 5 + 3		= 8
	2		2

b) Ciąg geometryczny (b_n):

	3
b1 =		,
	2

	3		2
b4 = 12 ⇒		q3 = 12 / *		⇒ q3 = 8 ⇒ q = 3√8 = 2,
	2		3

	3
b2 = b1*q = c =		* 2 = 3,
	2

b₃ = b₂*q = d = 3 * 2 = 6.

	1
Odp.: a = 5, b = 8		, c = 3, d = 6.
	2

Bogdan: Życzę piszącym wkrótce egzamin pomyślności

AROB: Super praca i niezwykle wartościowy materiał edukacyjny! Dziękuję w imieniu wszystkich potrzebujących (ja niestety potrzebowałam to kilkadziesiąt lat temu).

Eta: Witam Bogdanie Potwierdzam słowa AROB . Zad. 4 w jego końcowej wersji policzyłam tak: cena po dwukrotnej obniżce; 150 *0,8*0,85 = 150*0,68 = 102 zł zatem : 100%−68% = 32% Odp: cena marynarki po dwukrotnej obniżce wynosi 102 zł i jest niższa od pierwotnej ceny o 32% Miłych snów

Eta: Przepraszam Bogdanie , w zad. 6 wkradł się chochlik. B: x ⊂ ( −∞, √2>

Eta: Podobnie na osi dla x = √2 ... kółeczko powinno być zamalowane. PS; Mam nadzieję ,że się nie pogniewasz za te uwagi

Bogdan: Dzień dobry. Nie, nie ma błędu. Kółeczek nie trzeba zamalowywać. Sposób zaznaczania przedziałów jest tym zagadnieniem, z którym walczę prawie całe dorosłe życie. Ci, którzy mieli okazję uczyć matematyki, wiedzą z doświadczenia, że o ile suma i iloczyn przedziałów nie sprawiają uczniom kłopotów, to różnice − tak. Uczeń nie zawsze potrafi do właściwej strony przypisać punkt z zamalowanym kółeczkiem. Jak różne zresztą spotyka się u nauczycieli i w podręcznikach sposoby zaznaczania przedziałów liczbowych, a to kółeczko zamalowane, a to kółeczko nad osią, a to pochylona kreska, itd. Przyznam się, że biorąc podręcznik do ręki, sprawdzam najpierw, jak autorzy zaznaczają przedziały, jeśli kółeczka są u nich zamalowane − nie kupuję takiego podręcznika. Czym jest przedział domknięty w jakimś punkcie x₀? To przedział zawierający ten punkt, rysujmy więc ten punkt wewnątrz przedziału. A czym jest przedział otwarty w punkcie x_o?. To przedział nie zawierający tego punktu, rysujmy więc ten punkt poza przedziałem. Taki sposób zaznaczania przedziałów wyraźnie pokazuje położenie punktu i tu uczniowie widzą, czy przedział w punkcie x_o jest otwarty, czy domknięty. Rysunek ma przecież pomagać zrozumieć zagadnienie, jego oznaczenia nie mogą być różnie interpretowane i nie mogą powodować błędnych odpowiedzi. Taką właśnie niejednoznaczność powoduje zamalowywanie punktów przy przedziałach domkniętych. Namawiam do rysowania wyłącznie pustych kółeczek, pionową kreską określamy położenie kółeczka, kółeczko jest przecież odzwierciedleniem punktu na osi. Taki rysunek jest najprostszy z możliwych i najbardziej czytelny. Przykłady (rysunki): a) x ∊ <2, 5>, b) x ∊ (2, 5), c) x ∊ <2, +∞) d) x ∊ (−∞, 5) e) x ≠ 2 f) A = (2, 5>, B = (3, 8>, wyznaczyć sumę, iloczyn, różnice przedziałów A, B. A∪B = (2, 8> A∩B = (3, 5> A \ B = (2, 3> B \ A = (5, 8>

AROB: Dzień dobry. Rzeczywiście ciekawy i przekonujący to sposób zaznaczania przedziałów. Przyznam jednak, że mając do czynienia z podręcznikami wielu wydawnictw, nie spotkałam się z taką interpretacją. Czy to może pomysł autorski? Na pewno godny wykorzystania, ale jak to zrealizować, gdy nauczyciele opierają się na symbolice stosowanej w powszechnie używanych podręcznikach? Dziękuję i pozdrawiam.

Bogdan: To jest właśnie zdroworozsądkowe podejście do zagadnienia. Jeśli przedział jest w punkcie x_o domknięty, to niech na rysunku będzie widać, że punkt x_o jest wewnątrz przedziału i jest skrajnym punktem. Jeśli przedział jest w punkcie x_o otwarty, to trzeba pokazać na rysunku (rysunek ma przecież pomóc zrozumieć), że x_o jest poza przedziałem i jest styczny do przedziału. Już kiedyś wyraziłem tu pogląd o poziomie nauczycieli, którzy wtłaczają w umysły uczniów schematy, klucze, szablony, nie ucząc myślenia. Różnorodność oznaczeń przedziałów spotykanych w podręcznikach świadczy o nieujednoliconej symbolice tego zagadnienia w literaturze. Wybrałem ten sposób, bo moim zdaniem jest czytelny. Jeszcze raz podkreślam − rysunek ma pomóc, a nie wzbudzać wątpliwości.

Bogdan: Witaj Eto , widzę, że jesteś. Jestem ciekaw Twojej opinii o sposobie zaznaczania przedziałów, który tu przedstawiłem i który wszędzie, gdzie się da, polecam.

Eta: Hmm.... to mi się dostało ! Z pewnością nie byłam tak wybitnym nauczycielem jak Ty Bogdanie, ale i nie najgorszym. Postaram się by w przyszłości nie czynić żadnych uwag tego typu. Jeżeli swoją obecnością na tym forum więcej szkodzę niż pomagam ( w Twojej ocenie) to wypada mi delikatnie wycofać się . Przepraszam , pozdrawiam i życzę miłego dnia

Bogdan: Ależ Eto, bardzo sobie cenię Twoje uwagi i wiem, że jesteś świetnym nauczycielem, o czym świadczą liczne na tym forum słowa wdzięczności skierowane pod Twoim adresem. Przez myśl mi nie przeszło zakwalifikować Ciebie do osób udzielających wsparcia, ale ograniczających się do schematów. Wielokrotnie widziałem Twoje nowatorskie podejście do zamieszczanych tu zadań i podziwiam Twoją życzliwość i cierpliwość okazywaną szukającym tu pomocy. Krytykę dotyczącą zaznaczania na rysunku przedziałów liczbowych skierowałem w stronę stosowanych sposobów. Staramy się przecież znaleźć taką prezentację materiału, by była ona jak najbardziej sprzyjająca jego zrozumieniu i pomagająca w rozwiązaniu zadań. Bardzo mi przykro, że tak odczytałaś moje słowa. Mam nadzieję, że jeszcze nie raz będziemy zażarcie dyskutować o różnych problemach związanych z naszym ukochanym przedmiotem. Pozdrawiam serdecznie