a kasiaaa: oblicz sin2x oraz cos 2 x jeśli tgx=−3 i xe (π/2,π)

PW: cos2x=cos²x−sin^x, po podzieleniu tej równości przez 1=sin²+cos^x dostajemy:

	cos2x		cos2x−sin2x
		=
	1		sin2x+cos2x

	cos2x		sin2x
cos2x=		−		.
	sin2x+cos2x		sin2x+cos2x

W pierwszym ulamku dzielimy licznik i mianownik przez cos²x, w drugim przez sin²x:

	1		1
cos2x =		−		.
	tg2x+1		1+ctg2x

	1
Wystarczy podstawic tgx=−3 i ctgx=−		i zastanowic sie czy istotna jest informacja o
	3

przedziale, do ktorego nalezy x. Poradzisz sobie z obliczeniem sin2x?

PW: W drugiej linijce oczywiscie sin²x+cos²x − dwojka w potedze zniknela.

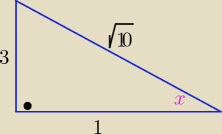Eta: tgx=−3 x€ II ć. to sinx >0 i cosx <0

	3		3√10		1		√10
sinx=		=		cosx= −		= −
	√10		10		√10		10

	3√10		√10		3
sin2x= 2sinx*cosx = 2*		*(−		)= −
	10		10		5

	4
cos2x= 2cos2x −1= ........= −
	5

Eta: