geometria analityczna camel: Dany jest okrąg o równaniu x²+2x+y²=9 . Punkt A=(−2,3) jest wierzchołkiem kwadratu ABCD wpisanego w ten okrąg. Wyznacz współrzędne wierzchołka B i C ogólnie rzecz biorąc mam sposób na to zadanie, mianowicie poprzez układ dwóch równań okręgów. Z danego danych w zadaniu wyliczam ze r²=10 a wiedząc ze to kwadrat wpisany w te koło to mogę wyliczyć bok: a2^1/2=2^1/2 * a z tego wychodzi ze a=pierw z 20 i z tond powstaje mi drugie koło o równaniu (x+2)²+(y−3)²=20 a drugi okrąg to (x+1)² +y²=10 i pkt w których się przetną to dwa wierzchołki. Lecz niestety coś nie gra. Proszę o pomoc

Fixed: Wyznacz wspolrzedne srodka okregu to z wektorow obliczysz wierzcholek C.

Skipper: ... a te "z tond" to pokaż swojemu poloniście −

Fixed: A w zasadzie to latwiej obliczyc z srodka odcinka − punkt S(srodek okregu) jest srodkiem odcinka AC, a ztego to latwo obliczysz wierzcholek C. Ponziej liczysz rownnaie proctej AC i prostej prostopadlej do niej OB. Pozniej z ukladu rownan okregu i prostej OB doliczysz 2 pozostale wierzcholki. Ale chetnie poznałbym tez jakis inny sposob, moze jest cos latwiejszego?

camel: oj tam oj tam czepisz się Skipper z ortografii nigdy nie byłem najlepszy a jest któryś z was chętny to policzyć ? bo za wszelką cenę chce policzyć to "swoim sposobem" ale widocznie gdzieś robię błąd

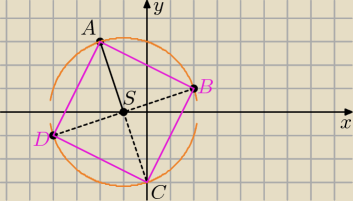
Mila: x²+2x+y²=9 . Punkt A=(−2,3) jest wierzchołkiem kwadratu ABCD wpisanego w ten okrąg. (x+1)²+y²=10 S=(−1,0), r=√10 S jest środkiem odcinka AC, korzystam z wzoru na wsp. środka odcinka C=(x_c,y_c)

	−2+xc		3+yc
−1=		i 0=
	2		2

stąd : x_c=0 i y_c=−3 C=(0,−3) przekątne w kwadracie są prostopadłe i równe, dzielą się na połowy. SA^→⊥SB^→ SA^→=[−1,3] ⇒SB^→=[3,1] S=(−1,0] →translacja o wektor SB^→=[3,1] i mamy B=(−1+3,0+1)=(2,1) S=(−1,0] →translacja o wektor (−SB^→)=[−3,−1] i mamy D=(−1−3,0−1)=(−4,−1) II sposób na wyznaczenie wsp. B i C Piszesz równanie prostej AS; Piszesz równanie prostej BS⊥AS; Znajdujesz wsp. punktów przecięcia z okręgiem, ale to trochę więcej pracy.

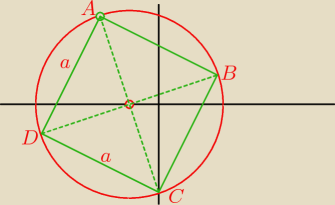
Skipper: ... popatrz na rysunek ... Twój sposób ma błąd w założeniach z punktu A chcesz zatoczyć okrąg o promieniu a√2 a przecież punkty B i D są odległe od A ... o a a nie o a√2

camel: nie nie Skipper Ja z pkt A chce zataczać okrąg o promieniu a a Jak to jest z tymi wektorami jeśli są do siebie prostopadłe ?

Skipper: ... jeśli o promieniu a ... to z przecięcia się okręgów oczywiście wyznaczysz współrzędne punktów B i D

camel: tak tak . tylko coś mi nie wychodzi. a liczenia w cholerę. ale założenie ok.Teraz patrząc w oparciu o Twój rys jakbym chciał to robić wektorami to powinienem wyznaczyć wektor AC. Ale jak potem wyznaczyć wektor DB ? ja zawsze wszystko robiłem prostymi nie wektorami

Mila: u=[a,b] v⊥u, to v=[b,−a] albo v=[−b,a] 2) a=2√5 (x+2)²+(y−3)²=20 a drugi okrąg to (x+1)² +y²=10 x²+4x+4+y²−6y+9=20 x²+2x+1+y²=10 odejmuję stronami 2x−6y=−2 x−3y=−1 x=−1+3y podstawiam do drugiego rownania (−1+3y+1)²+y²=10 (3y)²+y²=10 y²=1 y=1 lub y=−1 x=−1+3*1=2 punkt (2,1) lub x=−1+3*(−1)=−4 punkt ( −4,−1)

camel: a to dzięki Mila za objaśnienie z tymi wektorami. tylko równania z okręgami robiłem troszeczkę inaczej: z jednego wyliczyłem y i podstawiłem do drugiego. A powiedz mi Mila jeszcze jak to jest z wektorami które są do siebie równoległe ?

Mila: 1) równania z okręgami lepiej moim sposobem, redukujesz wyrazy: x² i y², otrzymujesz równanie liniowe. 2) u^→=[a,b] v^→||u^→ v^→=[a,b] albo v^→=[k*a,k*b], k− liczba

camel: no w sumie tak u mnie sporo liczenia ok dzięki za pomoc

Mila: powodzenia.