proszę o rozwiązanie zaraza: Wyznacz największe ujemne rozwiązanie równania sin(−2x)=sinx.

Skipper: funkcja sinus jest nieparzysta więc sin(−2x)=−sin2x zatem: sinx+sin2x=0 sinx(1+2cosx)=0

	1
sinx=0 lub cosx=−		....dalej sobie "dośpiewaj" −
	2

zaraza: Właśnie z tym dalej mam problem wychodzi mi 2/3π +2kπ oraz 4/3π+2kπ a te wartości nie są ujemne

Skipper: ... to odpowiedz sobie na pytanie co to jest największe ujemne −

zaraza: Mógłby mi Pan podać pełne rozwiązanie zadania?

Skipper: a odpowiesz na postawione pytanie "największa ujemna" ... ujemna ale najbliższa 0 ....czyli ? Popatrz na wykres cosinusa ...

pigor: ..., czyli szukane rozwiązanie leży "najbliżej" zera z jego lewej strony, a więc dla jakiej wartości k spośród k=±1,±2, . .. ...

zaraza: −1/2π

Skipper: ... oczywiście rozwiązaniem jest tylko jedna wartość x Dla sinx=0 największą ujemną wartością x byłoby −π dla cosx=−1/2 największą ujemną wartością x jest −(π/2+π/6) czyli x=−2/3π Zauważ, że policzysz to również z Twojego 4/3π+2kπ podstawiając k=−1 czyli −2π+4/3π=−2/3π

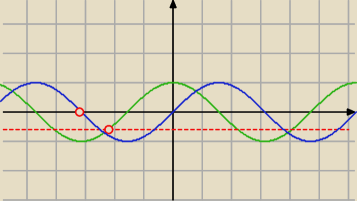
Skipper: ... tak lepiej?