Ostrosłupy - zadania
Meg: Ostrosłupy − zadania
1. W ostrosłupie prawidłowym czworokątnym powierzchnia boczna jest nachylona do powierzchni
podstawy pod katem 60 stopni , a krawedz podstawy ma dlugość 16cm. Oblicz pole powierzchni
całkowitej i objetosc tego ostrosłupa
2. W ostrosłupie prawidłowym czworokątnym przekatna podstawy ma dlugosc 6
√2 a krawedz boczna
tworzy z płaszczyzna podstawy kat 30stopni. Oblicz pole powierzchni całkowitej i objętość tego
ostrosłupa
3. W ostrosłupie prawidłowym czworokątnym krawędź boczna długości 10cm tworzy z krawędzią
podstawy kat 60stopni. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.
Proszę o pomoc w rozwiązaniu tego zadania.
dziękuje
9 mar 12:35
Meg: pomoże ktoś? proszę
9 mar 13:05
Janek191:
z.1
Powinno być ściana boczna.
α = 60
o
a = 16 cm
0,5 a = 8 cm
h − wysokość tego ostrosłupa
Mamy
więc
h = 0,5 a* tg 60
o = 8 cm *
√3 = 8
√3 cm
=========================
Objętość ostrosłupa
| | 1 | | 1 | | 1 | | 2 048 | |
V = |
| Pp *h = |
| a2 * h = |
| 162 * 8 √3 = |
| √3 |
| | 3 | | 3 | | 3 | | 3 | |
==============================================
h
1 − wysokość ściany bocznej ( trójkąta równoramiennego )
Mamy
Pole powierzchni ostrosłupa
P
c = P
p + P
b = a
2 + 4*0,5 a*h
1 = a
2 + 2a*h
1
więc
P
c = 16
2 + 2*16*16 = 256 + 512 = 768
================================
| | 2 048 | |
Odp. Pc = 768 cm2, V = |
| √3 cm3 |
| | 3 | |
=======================================
9 mar 15:09
Janek191:
z.2
a − długość krawędzi podstawy ostrosłupa ( kwadratu )
Mamy
a
√2 = 6
√2 ⇒ a = 6
b − długość krawędzi bocznej ostrosłupa
α = 30
o
x − długość połowy przekątnej podstawy
x = 3
√2
Mamy
b
√3 = 6
√2
cdn. później − przyszli goście
9 mar 15:19
Meg: dziękuje Ci Janku za pomoc
*
czekam na 3 zadanie
9 mar 16:01
dero2005:
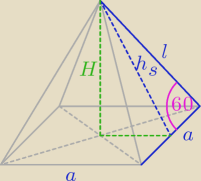
l = 10
a = l = 10
h
s =
√l2 − (a2)2 =
√102 − 52 =
√75 = 5
√3
H =
√hs2 − (a2)2 =
√(5√3)2 − 52 =
√50 = 5
√2
P
c = a
2 + 2a*h
s = 100(1 +
√3) cm
2
| | a2*H | | 102*5√2 | | 500 | |
V = |
| = |
| = |
| √2 cm3 |
| | 3 | | 3 | | 3 | |
9 mar 19:21
Janek191:
cd. z. 2
| | 6 √2 | | 6 √2* √3 | |
b = |
| = |
| = 2 √6 |
| | √3 | | √3* √3 | |
h − wysokość ostrosłupa
Mamy
h
2 = b
2 − x
2 = ( 2
√6)
2 − ( 3
√2)
2 = 24 − 18 = 6
więc
h =
√6
=======
h
1 − wysokość ściany bocznej
h
12 = h
2 + ( 0,5 a)
2 = 6 + 3
2 = 6 + 9 = 15
więc
h
1 =
√15
=============
Objętość ostrosłupa :
| | 1 | | 1 | | 1 | |
V = |
| Pp * h = |
| a2 * h = |
| * 62 * √6 = 12 √6 |
| | 3 | | 3 | | 3 | |
======================================
Pole powierzchni
P
c = P
p + P
b = a
2 + 4* 0,5 *a*h
1 = a
2 + 2a*h
1
więc
P
c = 6
2 + 2 *6*
√15 = 36 + 12
√15 = 12*( 3 +
√15)
=======================================
z.3 rozwiązał dero2005
9 mar 21:02
Bogdan:
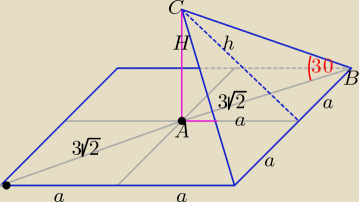
Zadanie 2. a
√2 = 3
√2 ⇒ a = 3 ⇒ 2a = 6
Korzystając z własności trójkąta prostokątnego, którego miara kata ostrego jest równa 30
o
| | √3 | |
w trójkącie ABC otrzymujemy: H√3 = 3√2 /* |
| ⇒ H = √6 |
| | 3 | |
Z twierdzenia Pitagorasa h =
√H2 + a2 =
√6 + 9 =
√15
| | 1 | |
Objętość V = |
| *62*√15 = 12√15 |
| | 3 | |
Pole P
c = 36 + 4*3*
√15 = 36 + 12
√15 i tyle
9 mar 21:56
Bogdan:
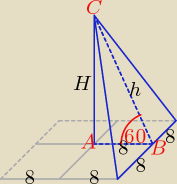
Zadanie 1:
Korzystając z własności trójkąta prostokątnego, którego miara kata ostrego jest rowna 60
o
w trójkącie ABC otrzymujemy: h = 2*8 = 16, H = 8*
√3
| | 1 | | 2048 | |
Objętość V = |
| *162*8√3 = |
| √3 |
| | 3 | | 3 | |
Pole P
c = 16
2 + 4*8*16 = 768 i już
9 mar 22:10