Stereometria, kula, stożek Licealista D: Pole podstawy stożka jest trzy razy mniejsze od pola jego powierzchni bocznej. Wykaż, że promień kuli wpisanej w ten stożek jest równy R = ^r√2₂ , gdzie r jest promieniem podstawy stożka.

Licealista D: πrl = 3πr² 3r = l −−−−−−−−−−−−−−−−−−−−−−−− W odpowiedziach jest podane, że trzeba skorzystać z podobieństwa

r		R
	=
l		√ l2− r2 −R

Licealista D:

	r		R
Ale ja dochodzę do		=
	√l2−r2		√l2−r2−R

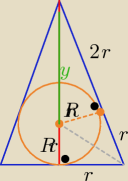
Eta: h²= 9r²−r² ⇒ h=2r√2 y=h−R=..... =2r√2 −R

	r		r		1
		=		=
	l		3r		3

R		1		r√2
	=		⇒ R=....... =
2r√2−R		3		2

dero2005: P_p = πr² P_b = πrl 3*P_p = P_b 3πr² = πrl l = 3r H = √l² − r² = √9r² − r² = 2r√2

r		R
	= sin α =
l		H−R

r		R
	=
l		r2√2 − R

r*(r2√2−R) = 3r*R |:r r*2√2 − R = 3*R r*2√2 = 4R

	r*2√2		r√2
R =		=
	4		2

Licealista D: I znowu wielkie dzięki Dero.

Eta:

jikA: To ja podziękuję również Eta Tobie za rozwiązanie bo Licealista D chyba zapomniał albo nie widział Twojego rozwiązania.

Eta: dzięki

Licealista D: Nie zauważyłem, odrazu skupiłem uwagę na ostatnim. Oczywiście dziękuję Eta również