Styczne i sieczne do okręgu Krystian: Punkty Q, R, S leżą na okręgu o środku O i promieniu r. Styczna do okręgu w punkcie Q przecina prostą RS w punkcie P. Oblicz r jeśli |PR|=|RS|=4√2 oraz |PO|=10

Eta: r=6

Janek191: PR *PS = PQ² = 10² − r² 4√2 * 8 √2 = 100 − r² 64 = 100 − r² r² = 100 − 64 = 36 r = 6 ==========

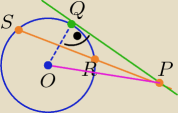
Eta: Z twierdzenia o stycznej i siecznej okręgu: |PQ|²= |PS|*|PR| i z treści zadania: |PR|=|RS| to |PS|=2|PR| zatem: |PQ|²= 2|PR|²= 64 ⇒ |PQ|=8 Z trójkąta prostokątnego POQ z tw. Pitagorasa oblicz długość "r"