dwa kółka Abdul: Hardkor 9.148. Odległość środków dwóch kół o jednakowych promieniach długości r, jest równa r. Oblicz pole części wspólnej tych kół.

Basia: Pomagam

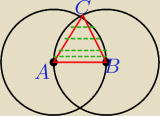
Basia: szukane P = 2*P_{obszaru ABC} (zielona linia przerywana) |AC|=|BC|=|AB|=r bo AC i BC to promienie okręgów, AB odległość między środkami ⇒ △ABC jest równoboczny P_{obszaru ABC}=P_{wycinka CAB}+P_{wycinka ABC}−P_△ABC

	πr2
Pwycinka CAB=Pwycinka ABC =
	6

	r2√3
P△ABC=
	4

	πr2		r2√3
Pobszaru ABC=2*		−		=
	6		4

πr2		r2√3
	−		=
3		4

4πr2−3r2√3		r2
	=		*(4π−3√3)
12		12

	r2		r2
P = 2*		*(4π−3√3) =		*(4π−3√3)
	12		6

Abdul: Dzięki , najpierw nie wiedziałem dlaczego odejmowałaś pole trójkata ale już wszystko wiem

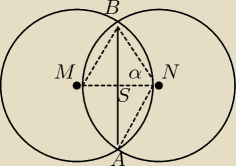
AS: Podaję inną wersję rozwiązania: α = 60^o , αr = π/3 [rad] Podc.ABM = Pwyc.NBMAN − PΔABN

	1		1		π*r2
Pwyc.NBMAN =		*r2*2*αr =		*r2*2*π/3 =
	2		2		3

	1		1		√3		r2*√3
PΔABN =		*r2*sin(2*α) =		*r2*		=
	2		2		2		4

	π*r2		r2*√3		r2
PodcABM =		−		=		*(4*π − 3*√3)
	3		4		12

Szukane pole S = 2*PodcABM

	r2
S =		*(4*π − 3*√3)
	6

Abdul: też ciekawe Dzięki za zainteresowanie

jdhbcjd: Nakręciliście na maxa Najprościej to 2 razy pole trójkątów równobocznych o boku r plus 4 razy pole odcinka koła (pole wycinka o kącie środkowym 60stopni − pole trójkąta) Czyli pole cz.wspólnej, to: 4*(πr²/6 − r²√3/4)+2*r²√3/4 Z całym szcu. ale sposób Basi zupełnie do mnie nie przemawia...

Artur_z_miasta_Neptuna: albo inaczej: wycinek koła (1/3 całości) − trójkąt równoramienny o ramionach 'r' i kacie 120^o ... czyli wysokości r/2 to *2 i macie wynik to już któreś tego typu zadanie w ciągu ostatnich 3−4 dni