Ostrosłup Licealista D: Podstawą ostrosłupa jest trójkąt prostokątny ABC o przeciwprostokątnej 12 i kącie ostrym 30stopni. Wszystkie krawędzie boczne są nachylone do płaszczyzny podstawy pod kątem 60 stopni. Wyznacz objętośc tego ostrosłupa. Nie wiem jak wyznaczyć H.

Licealista D: Kto orientuje się w stereometrii?

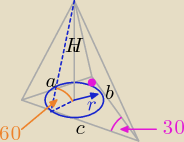
dero2005: c = 12

a
	= sin 30o = 12
c

a = 6

b		√3
	= cos 30o =
c		2

b = 6√3

r		a*b
	(a + b + c) =
2		2

r = 3√3 − 3

H
	= tg60o = √3
r

H = r√3 = 9 − 3√3

	a*b*H
V =		=
	6

Licealista D: Nie tak, kąt jest nie od ściany bocznej, a od krawędzi ściany bocznej. Wynik powinien być 6√3 , nie sądze, by w odpowiedziach była pomyłka.

dero2005: Moja wina, źle doczytałem − poczekaj

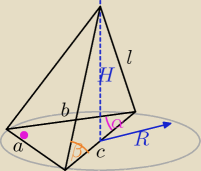
dero2005: c = 12 α = 30^o β = 60^o

	c
R =		= 6
	2

a		1
	= sin 30o =
c		2

a = 6 b = √c² − a² = √144 − 36 = √108 = 6√3

H
	= tg 60o = √3
R

H = R*tg60^o = 6√3

	a*b
Pp =		= 18√3
	2

	Pp*H
V =		=
	3

Licealista D: Fakt, dzięki wielkie. Nigdy bym nie wpadł, żeby opisać okrąg .. Ale teraz będę pamiętał.

Licealista D: Ale teraz mam zastanowienie, czemu wysokość H pada na krawędź c .?

Licealista D: Bo jak są nachylone do płaszczyzny podstawy pod kątem 60 stopni więc wysokośc powinna padać gdzieś w trójkącie?

Licealista D: Nikt nie potrafi pomóc?

konda: Jeśli wszystkie krawędzie tworzą z podstawą jednakowy kąt to spodek wysokości leży na środku przeciwprostokątnej. Warto zapamiętać!

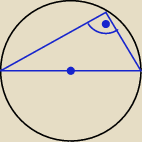
dero2005: jeżeli ostrosłup jest prawidłowy prosty to na podstawie można opisać okrąg. jeżeli na trójkącie prostokątnym opiszesz okrąg to środek okręgu wypadnie dokładnie na środku przeciwprostokątej przypomnij sobie właściwości kąta środkowego opartego na średnicy

Licealista D: "Jeśli wszystkie krawędzie tworzą z podstawą jednakowy kąt to spodek wysokości leży na środku przeciwprostokątnej. Warto zapamiętać!" − o właśnie o to chodziło Dzięki Wam