Wiola Wiola: Zad. 5 Wykaż, że nie istnieje kąt alfa, taki, że cos (alfa) α= 3/5 i tg α = 3/4.

konda:

	sinα
tgα=
	cosα

wyliczasz sinα i potem do wzoru: sin²+cos²=1

Wiola: dzięki spróbuje dalej sama wyliczyć: tgα = sinα/cosα /*cosα sinα= tgα * cosα ⇒ sinα= 3/4 * 3/5 ⇒sinα=9/20 sin²α + cos²α = 1 (9/20)² + (3/5)² =1 81/400 + 9/25 =1 81/400 + 144/400 =1 225/400 ≠ 1 Czy tak to miało być rozwiązane? Czy to już koniec zadania? Ktoś może to sprawdzić? Z góry przepraszam za zapis ale nie wiem jak wstawić ułamek

Eta:

	3		4		3
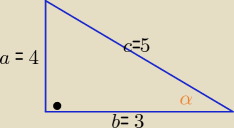
Jeżeli cosα=		to tgα=		≠
	5		3		4

czyli taki kąt α nie istnieje

krystek: Dobrze, nie widze błędu. Duże U

81
400

Wiola: Dziękuje