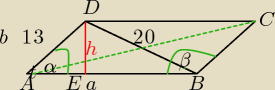
geometria Magda: W równoległoboku tangens kąta ostrego jest równy 2,4. Krótszy bok ma długość 13, a krótsza przekątna 20. Oblicz długość dłuższej przekątnej.

Mila:

	24
tgα=
	10

	sinα		12		12
tgα=		=		⇔sinα=		cosα
	cosα		5		5

Z jedynki trygonometrycznej:

	12
(		cosα)2+cos2α=1
	5

144
	cos2α+cos2α=1
25

169
	cos2α=1
25

	25		5
cos2α=		stąd cosα=		>0 dla ostrego kąta
	169		13

Z tw. cosinusów w ΔABD: 20²=a²+13²−2*a*13 cosα

	5
400=a2+169−26*		a
	13

231=a²−10a ⇔a²−10a−231=0, Δ=100+924=1024,√1024=32

	10−32
a=		<0 nie odpowiada warunkom zadania
	2

lub

	10+32
a=		=21
	2

a=21

	5
β=180−α, cos(180−α)=−cosα=−
	13

Z tw. cosinusów w ΔABC:

	5
|AC|2=212+132+2*21*13*
	13

dokończ i poprzeliczaj wszystko

Magda: Dziękuję

Mila:

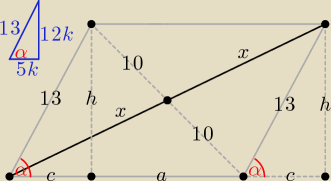
Bogdan: Proponuję takie rozwiązanie:

	24		12
tgα =		=		, (5k)2 + (12k)2 = 132 i k∊N ⇒ 169k2 = 169 ⇒ k = 1
	10		5

h = 12k = 12, c = 5k = 5, a = √20² − 12² = √256 = 16, a + 2c = 26 2x = √26² + 12² = √820 = 2√205

Szlupek: A czy to nie h=5 a c=12?

Szlupek: A nie, mój błąd.

Eta:

	h		12
tgα=		=		⇒ h=12 , c= 5
	c		5