Okrąg hwdtel: Udowodnić że promień okręgu stycznego równocześnie do dwóch prostych

	|b1−b2|
równoległych: k; y=mx + b1 i l: y=mx + b2 wyraża wzór R=
	2√m2+1

A jak nie potrafisz to nie pchaj się na afisz

Mateusz: Okrąg styczny do obu prostych będzie miał średnicę długości odległości pomiędzy tymi prostymi.

	|b1−b2|
R=		wiec to zadna filozofia
	√1+m2

hwdtel: Czyli proste jak ta dygnitarska krowa ,ale...pozostaje jeszcze wykazanie wzoru

	|b1−b2|
2R=		,mądralo !
	√m2+1

Licealista D: Właśnie to wykazał ... Ze wzoru na odległość punktu od prostej

hwdtel: Z takimi "rewolucjami"to ty licealista uciekaj z powrotem do telewizji,a na forum dopiero po zdaniu matury (,co moze ci się wyjątkowo udać) z taką kondycją inteligencką! ,bo na studiach możesz tylko zaliczyć kulkę i cisza na morzu wicher dmie

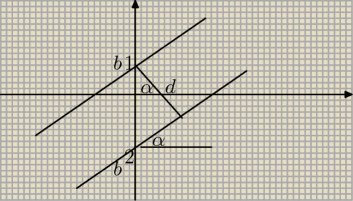
Radosław: Przerwiemy ciszę!Rzadko zaglądam na strony internetowe bo faktycznie roi się na nich od technicznie uprzywilejowanych "stróżów prawomyślnosci" inwigilujących internet.Ale do kochanej starej budy czasami warto zajrzeć!Oczywiście nie jestem pedagogiem,nie znam układów podręczników szkolnych,ale przypuszczam,że faktycznie dość trywialny dowód powyższego równania ,który te podręczniki zawierają mógłby wyglądać mniej więcej tak:

d		1
	=cosα ⋀ tgα=m (czyli cosα=		)
|b1−b2|		√m2+1

Eta: Do tego jeszcze .... śnieg pada

Radosław: ciąg dalszy nastąpi [ to jak licealista −zawierają dokładnie?],słowem ten mądrala mateusz całkiem niegłupi Rzecz w tym,że dowód na tę zależność może również wyglądać tak: K(−b1m;0}∊k ⋀ P(−b2mt;−b2t+b2})∊l ⋀ L(−b2mt0;−b2t0+b2)∊l d=2R=( [xL−xK]2 +[ yL−yK]2)0,5,czyli d'(t)=0⇔t=t0=tminimum,itd To jak licealista−takiego wywodu podręczniki szkolne nie zawierają c.d.nastąpi

Mila: Nie, nie zawierają, bo w LO nie ma pochodnych, a dowód jest banalny bez pochodnych i nie ma co się popisywać i kpić z ucznia. Proszę nie zaśmiecać forum takimi komentarzami. To jest forum dla tych, którzy chcą się czegoś nauczyć i tych, którzy chcą pomóc.

Radosław:

	b2m2 + b1
d=([b1m−b2mt]2 +[ −b2t+b2]2)0,5,czyli t=to=		,
	b2(m2+1)

czyli po podstawieniu za t (zastanawiając się dłużej nad tym że [(x−y)]²=[(y−x)]²),powinno się zgodzić! Możliwość sprawdzenia pozostawiam np:Ecie[na której ręce zasyłam jednocześnie pozdrowienia dla wszystkich komputerowych dygnitarzy]−(a nóż jakiś chochlik) To takie moje szkolne deja vou.Już znikam.cd nie nastąpi

Eta:

:: :

Mateusz: Ten gośc ma rozdwojenie wiadomo czego nie dziwota ze potem są "Panie" Anie w sejmie Tak przy okazji Wszystkiego najlepszego wszystkim Paniom na tym forum

KobiEta: