Styczna met: Wykaż, że prosta x+2y−4=0 nie jest styczna do okręgu o równaniu x²+y²−4x+3=0. Doprowadziłam już równanie okręgu do postaci kierunkowej tj. (x−2)²+y²=1 Co powinnam zrobić dalej? Proszę o pomoc!

Skipper: ... do postaci kierunkowej powiadasz −

Dominik: (x − 2)² + y² = 1 x + 2y − 4 = 0 wyznacz x albo y z rownania prostej, wstaw do rownania okregu i policz Δ

ICSP: Wystarczy pokazać że odległość środka okręgu od prostej jest różna od promienia tego okręgu.

Skipper: Możesz to zrobić różnie: 1) układ równań ... nie ma rozwiązań ... prosta i okrąg nie mają punktów wspólnych jedno rozwiązanie ... styczna dwa rozwiązania ... prosta przecina okrąg 2) jeśli wykażesz że odległość środka okręgu od prostej nie jest równa promieniowi to prosta styczna nie jest

met: Wyszło, że Δ<0 czyli prosta i okrąg nie mają punktów wspólnych, tak? Tak, kanoniczna...

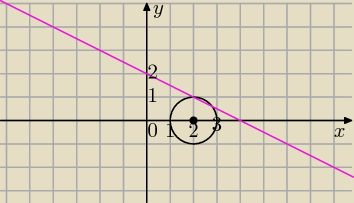
Mila: (x−2)²+y²=1 postać kanoniczna S=(2,0) współrzędne środka okręgu, r=1 promień okręgu k: x+2y−4=0 badamy odległość punktu S od prostej k

	|2+2*0−4|		2
d=		=		<1zatem ta prosta nie jest styczną lecz sieczną
	√12+22		√5