Pole trójkąta Marta: Narysowano trójkąt ostrokątny ABC, a następnie punkt A odbito symetrycznie względem punktu B, punkt B odbito symetrycznie względem punktu C, a punkt C odbito symetrycznie względem punktu A. Powstał trójkąt A'B'C'. Ile razy pole tego trójkąta jest większe od pola trójkąta ABC?

irena_1: Pole trójkąta ABC P_ABC=P Trójkąt AA'C' ma podstawę AA' 2 razy dłuższą niż AB. Odległość punktu C' od prostej AB jest taka sama, jak odległość punktu C od tej prostej, więc pole trójkąta AA'C' jest równe 2P. Podobnie− trójkąt CC'B' ma podstawę CC' 2 razy dłuższą niż odcinek AC, a odległość punktu B' od prostej AC jest taka sama, jak odległość punktu B od tej prostej, czyli pole trójkąta C'CB' jest równe 2P. Podobnie− pole trójkąta A'B'C jest równa 2P. Pole trójkąta A'B'C' jest więc równe: P+2P+2P+2P=7P. Pole otrzymanego trójkąta jest 7 razy większe od pola trójkąta ABC.

buzek: Wysokości tych trójkątów będą równe? Skąd to wiemy?

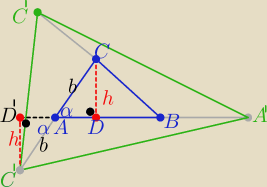
Eta: ... dlatego bo trójkąty ADC i AD^'C^' są przystające z cechy (kbk) zatem |CD|=||D^'C^'|=h

buzek: To może inaczej spytam. Mamy trójkąty ABC i AA'C'. W trójkącie AA'C' podstawa jest dwa razy dłuższa niż w trójkącie ABC. Jeden z boków jest taki sam (bo odległość punktu C' od prostej AB jest taka sama jak od punktu C). Dlaczego możemy na tym etapie wyciągnąć wniosek, że pole AA'C jest dwa razy większe od ABC?