Oblicz objętość tego ostorsłupa. Michu: Każda ściana ostrosłupa prawidłowego czworokątnego ma pole 8. Oblicz objętość tego ostrosłupa. Niby zadanie wydaję się proste ale za nic nie moge dojść do właściwego wyniku

Licealista: A jaki jest wzór na pole trójkąta równobocznego? Wydaje się proste i takie jest jak zna się wzory i twierdzenie pitagorasa.

Michu: Nie jestem głupi i podstawiałem wzór a²*√3/4 i wychodzi mi jakiś chiński wynik i z którym nic nie moge zrobić. Liczę, że znajdzie sie jakaś kompetentna osoba, która mi to zadanie wytłumaczy.

Licealista: Oj boże, sam jesteś niekompetentny. Oblicz polę okręgu wpisanego w ten trójkąt, potem wysokość dowolnej ściany. Otrzymasz prostą na dole i po skosie na górze. Z twierdzenia pitagorasa

	1
obliczysz wysokość całej bryły a jak masz wysokość całej bryły to pomnożysz ją przez
	3

wysokości. Zrób to co napisałem a rozwiążesz zadanie, nie licz na gotowca.

Michu: Dzięki za rady. NA Gotowca nawet nie liczę, jutro mam sprawdzian i próbuje ogarnąć wszystkie zadania, co mam w podręczniku, a w tym w ogole nie mogę dojść do wyniku. Tylko nie rozumiem z jakiej paki ma być wpisany okręg w trójkąt ? bo jednak jak by miał być wpisany to taka informacja powinna znaleźć się w zadaniu a jej nie ma.

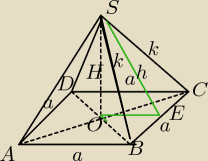
Mila: a²=8 a=√8=2√2

	1
PΔBCS=		a*h ( Δ nie musi być równoboczny, to nie wynika z treści)
	2

1
	*2√2*h=8
2

	8
h=		=4√2
	√2

z ΔSOE: H²+|OE|²=h² H²=(4√2)²−√2² H²=16*2−2 H²=30 H=√30

	1		8√30
V=		*8*√30=
	3		3

zadanie z Kiełbasy, jest tam błędna odpowiedź, chyba, że masz poprawione wydanie

Mila: Wszyscy uczniowie denerwują się przy tym zadaniu.