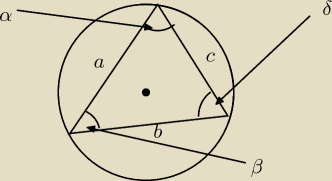
ołjea Kipic: Czwane rzadane mam takie "Czwane rzadane"

	4
α = cos −
	5

a =2 b=3√5 i teraz jak obliczyc reszte katow

	10√5
obliczylem ze sin δ =
	125

a jak obliczyc β i dlugosc c z czego po kolei mam korzystac prosze o pomoc

Eta:

	4
Napisz to porządnie ! co to jest za zapis : " α= cos −		" ? ... bez sensu
	5

Mila: Witaj, Eto, no widzisz co z nim mamy, a przecież chcemy go porządnie nauczyć. Pracowity, ale za szybko piszesz Kipic

Eta: Witaj Mila

Kipic: No dobra sorry chamskie to z mojej strony że nawet dobrze nie napisze ale poprostu mam lipną klawiature no to poprawiam:

	4
cos α = −
	5

a=2 b=3√5

	10√5
sin δ =
	125

Więc dalej nie wiem jak zrobić to aby wyliczyć β i długość c , zamotałem się i już nie wiem co po kolei czy lepiej z twiedzenia sinusów czy cosinusow Proszę o pomoc

Mila: 1) Po pierwsze , skoro cosinus ujemny to Δ jest rozwartokątny, rysunek będzie inaczej wyglądał, może to mieć znaczenie ( a może nie) Napisz od nowa treść, bo nie wiem co dane a co trzeba liczyć.

Kipic: Ja chcialem poprostu z grubsza sie nauczyc liczyc z twierdzenia cosinusów i sinusów ale treśc brzmi : Oblicz obwod trojkata ABC i promien okregu opisanego na tym trojkacie jezeli AB = 3√5 i AC = 2

	4
i cosinus kata ACB jest rowny −
	5

	5√5
Promien to latwo wyliczyc bo z twierdzenia sinusów wiec wychodzi		ale jak liczyc
	2

reszte katow i bokow

Skipper: ...np ... wzór na pole trójkąta i twierdzenie sinusów

Mila: Za pół godziny.

Kipic: z twierdzenia sinusów jak mozna wyliczyc c z RYSUNKU skoro ani nie ejst podany kat ani dlugosc CZWANE wzor na pole trojkata P= 2R² * sinα *sinβ * sinδ no tylko niemam sinδ więc wyznaczyć sin δ i potem mozna podstawic do twierdzenia sinusów i wyliczyc dlugsc sprawdze czy sie da

Skipper:

	1
PΔ=		absinα
	2

Kipic: no poleto jest obliczone wiec moge teraz wyznaczyc sin δ

Kipic:

	10√5
czyli sin δ =
	9

Kipic: chyba wkradl sie blad w oblicznia bo c wychodzi 5

konda: Po co sie bawic w pola, jak mozna obliczyc trzeci bok stosujac twierdzenie cosinusow

Skipper: ... bo On chyba sam nie bardzo wie co chce zrobić −

Kipic: no to sie pytam jak obliczyc bo nie wiem

Skipper: Kolego ... TY już raz któryś zmieniasz treść zadania i chyba sam nie wiesz co piszesz

Licealista D: Wykorzystuj twierdzenie cos, czyli: c² = a² + b² − 2abcosβ Podstawiasz tylko dane.

Kipic: przeciez od samego poczatku pisze jak obliczyc c myslalem ze jak policze pole to potem podstawie cos δ i wylicze to upragnione c ale dobra nikt mi nie chce odpisac tylko TLUMACZY NIEWIEM CO to nie. sam wkoncu dojde

Kipic: tez umiem wkleic twierdzenie cosinusow tylko niemam podanego kata cosβ a majac ulamki cosα i cosβ nie potrafie wyliczyc cosδ a pozatym jak podstawie to daje nam 2 niewiadome cos δ i c a z pola chcialem jedna niewiadoma cos δ uzyskac i podstawic

konda: W twierdzeniu cosinusów podstawiasz cos kąta zawartego miedzy dwoma danymi bokami. W Twoim przypadku masz dwa boki i kąt zawarty między nimi, więc nic nie szkodzi na przeszkodzie, żeby podstawić do wzoru. AB = 3√5 AC = 2

	4
cosinus kąta ACB (czyli między bokami, które masz dane) = −
	5

konda: Sorki, źle. AB = 3√5 AC = 2

	4
cosinus kąta ACB −
	5

BC = x AB² = AC² + BC² − 2AB*BC* cosACB Niewiadomą jest długość BC

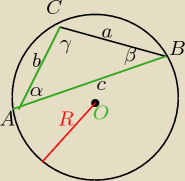
Mila: Pamiętaj, że we wzorach obowiązuje pewna zasada oznaczania boków w zależności od nazwy wierzchołków, Naprzeciw wierzchołkα A bok ma oznaczenie a, itd

	−4
|AB|=3√5, b=2 i cosγ=
	5

z jedynki trygonometrycznej obliczam sinγ, sinα>0 dla kąta ∊(0,180)

	−4		16
sin2γ+(		)2=1⇔sin2γ=1−
	5		25

	3
sinγ=
	5

	c		3√5
z tw. sinusów		=2R⇔		=2R
	sinγ		3/5

	5√5
R=
	2

b		2
	=2R⇔		=5√5⇔
sinβ		sinβ

	2
sinβ=
	5√5

Z tw. cosinusów: c²=a⁺b²−2b*a*cosγ⇔9*5=4+a²−2*2*a*(−4/5) i a>0 a=5 (drugi pierwiastek ujemny) jeszcze raz z tw. cosinusów a²=c²+b²−2*cbcosα 25=45+4−2*3√5*2cosα

	2
cosα=
	√5

trochę dziwne te liczby.

Kipic: Dziekuje Mila na Ciebie zawsze można liczyć

Mila: A skąd to zadanie?

Kipic: akurat to zadanie było w arkuszu maturalnym z nowej ery rozszerzenie