Wykaż że jeśli długości boków trójkąta są trzema kolejnymi wyrazami ciągu alm: Wykaż że jeśli długości boków trójkąta są trzema kolejnymi wyrazami ciągu arytmetycznego to długość promienia okręgu wpisanego w ten trójkąt jest równa jednej trzeciej długości jednej z wysokości tego trójkąta. A wiec mamy: −−−−−−−−−−−−−−−−−−−−−−−−− a=a₁ b=a₁+r c=a₁+2r 3R=h

	1
P=		ah
	2

P=Rp P=ah

	3h(a+r)
P=
	6

	3h(a+r)
ah=
	6

a+r=2a r=a Pytanie czy to jest dowód czy jeszcze nie?

PW: Nie. W "dowodzie" korzystasz z tezy − podstawiłes(aś) 3R=h − to co należało udowodnić. A końcowy wniosek to a=r (różnica ciągu równa najmniejszemu bokowi), a przecież o to nie pytali. Poza tym z góry założyłeś. że będzie to "h" opuszczona na bok "a" − skąd taka pewność?

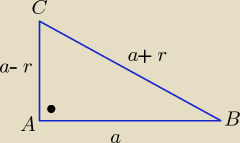
Eta: Można tak: r−− różnica ciągu arytmetycznego r€(0,a) i a>0 R_w −− dł. promienia okręgu wpisanego w ten trójkąt

	a*(a−r)
P=
	2

	2P		2P		a(a−r)
Rw=		=		=		=
	|AC|+|AB|+|BC|		a+a−r+a+r		3a

	1		1		1
=		(a−r) =		*|AC|=		*hAB
	3		3		3

PW: @Eta: Jako specjalista od niewygodnych pytań (nie raz dostałem za to po nosie w życiu) zapytam: a skąd wiedziałaś, że to trójkąt prostokątny?

Eta: Echh ... przeczytałam prostokątny