PRAWDOPODOBIEŃSTWO helplis : W urnie znajduje 10 kul. Jest X kul białych i Y kul czarnych. Jakie jest prawdopodobieństwo wylosowania dwóch tych samych kul. Z góry dziękuję!

Mila: Napisz treść zadania precyzyjnie, losowanie ze zwracaniem, czy bez, i co to znaczy tych samych kul, taki sam kolor?

helplis : Losowanie ze zwracaniem, wylosowanie dwóch kul jednego koloru.

Mila: Ω=10*10 Czy x+y=10? |A|=x*x+y*y

	x*x+y*y
P(A)=
	100

PW: Ω składa się ze wszystkich możliwych dwuelementowych ciągów (a,b), w których a i b mogą przyjmować wartości od 1 do 10. Przyjęcie takiego opisu gwarantuje, że wszystkie zdarzenia elementarne są jednakowo prawdopodobne (można stosować klasyczną definicję prawdopodobieństwa) i jest równoznaczne z ponumerowaniem kul, np. kule białe mają numery od 1 do X, a czarne od X+1 do X+Y, X+Y=10. |Ω|=10²=100. Zdarzenia A−wylosowano dwie białe kule i B−wylosowano dwie czarne mają liczność odpowiednio |A|=X² i |B|=Y². Zdarzenia te są rozłączne, więc P(A∪B) = P(A)+P(B), Odpowiedź: Prawdopodobieństwo, że obie kule są tego samego koloru jest równe

	X2+Y2
	102

PW: Mila,

Mila: Witaj, PW, jednoczesny wpis.

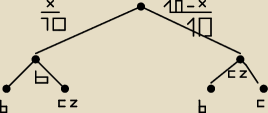
helplis : robiłem według takiego schematu i wszyło mi P(a) = − 2x + 10, nie wiem co ztym fantem zrobić, bo do pewnego momentu wiem że to jest dobrze, zatwierdzone przez nauczyciela, ale nie dokończonei nie wiem co z tym zrobić dalej.

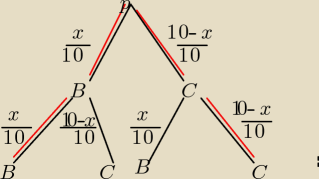
Mila: P(A) nie może mieć wartości większej niż 1. Jeśli dobrze opiszesz drzewko, to otrzymasz wynik podany wyżej. x+y=10 y=10−x,

	x		x		10−x		10−x
P(BB)+P(CC)=		*		+		*		=
	10		10		10		10

	x2+(10−x)2
=
	100

PW: Drzewka to zaraza rozpowszechniająca się w szkołach, chyba po to żeby wyrobić jakieś mechaniczne nawyki zamiast myślenia. W tym wypadku nie będziesz wiedział kiedy skończyć rysowanie, bo nie wiesz ile jest X, a ile Y. "Zatwierdzone przez nauczyciela"! Posługuj się własnym rozumem. Popatrz, co piszesz: "wyszło mi P(a) = −2x+10" − to znaczy, że gdyby x=4, to prawdopodobieństwo byłoby równe 2? Rozwiązanie zadania z rachunku prawdopodobieństwa powinno mieć określoną przestrzeń zdarzeń Ω (trzeba opowiedzieć, co jest zdarzeniem elementarnym) i zdefiniowane prawdopodobieństwo (najczęściej w szkolnym kursie jest to tzw. klasyczna definicja prawdopodobieństwa). Takie są wymagania programu i zdrowego rozsądku (muszę widzieć co liczę i według jakiej reguły). Zastępowanie sensu jakimiś gałęziami kończy się tragicznie. Drzewko − owszem, ale jako ilustracja, a nie jedyny sposób działania. Starałem się napisać rozwiązanie wedle reguł sztuki, choć mnie to nudzi. Przeczytaj jeszcze raz i nie daj się ogłupiać.

PW: Przepraszam, z tym "nie będziesz wiedział kiedy skończyć" to przesadziłem − są dwa losowania. Irytuje mnie to łamanie gałęzi tak, że zaczynam gderać.

Eta:

PW: O, ta ilustracja podoba mi się. Jest pogodna i na temat (to pośrodku to s t a r y g r z y b?)

Mila: Gałęzie powinny z rozpaczy opadać. A mnie pasjans nie wychodzi.

Eta: