Okrag
turek: Napisz rownanie okregu o promieniu dlugosci r=√5, wiedzac ze do okregu naleza punkty A=(5,1),
B=(1,3).
5 mar 19:29
Eta:
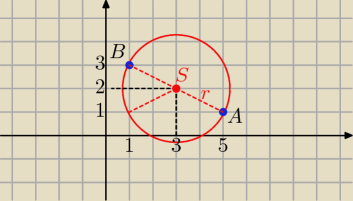 o: (x−3)2+(y−2)2= 5
o: (x−3)2+(y−2)2= 5
5 mar 21:21
Janek191:
Inny sposób:
A = ( 5; 1)
B = ( 1; 3)
r = √5
(x − a)2 + ( y − b)2 = r2
więc
( 5 − a)2 + ( 1 − b)2 = √52
( 1 − a)2 + ( 3 − b)2 = √52
−−−−−−−−−−−−−−−−−−−−−−−−−
25 − 10 a + a2 + 1 − 2 b + b2 = 5
1 − 2a + a2 + 9 − 6 b + b2 = 5
−−−−−−−−−−−−−−−−−−−−−−−−−−−− odejmujemy stronami
16 − 8 a + 4 b = 0 / : 4
4 − 2 a + b = 0
b = 2 a − 4
−−−−−−−−−−
10 − 2 a + a2 − 6*( 2a − 4) + ( 2 a − 4)2 = 5
10 − 2 a + a2 − 12 a + 24 + 4 a2 − 16 a + 16 = 5
5 a2 − 30 a + 45 = 0 / : 5
a2 − 6 a + 9 = 0
( a − 3)2 = 0
a = 3
====
b = 2*3 − 4 = 2
===============
Odp. ( x − 3)2 + ( y − 2)2 = 5
==========================
5 mar 22:09
 o: (x−3)2+(y−2)2= 5
o: (x−3)2+(y−2)2= 5