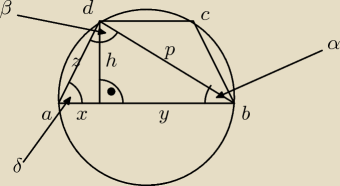
Oblicz promien okregu opisanego na trapezie jezeli ramie trapezu ma długosc 10cm dluzsza
podstawa 16cm a wysokosc 5√3 cm
wiec robilem tak :
oznaczylem :
h=5√3
x+y = 16
z= 10
wyliczylem :
najpierw x wyszedl 5 wiec x = 5 a y 11
i przekatna czyli p =14
potem z twierdzenia cosinusów102= 162+142−2*16*14 cos α
czyli cos α=U{11}{14
wyliczylem z jedynki trygonometrycznej sinα czyli wynosi 5√314
potem z twierdzenia sinusów
| 2R | 10 | |||||||||
czyli | = | |||||||||
| 1 |
|
| 70√75 | ||
i mi R = | ||
| 75 |
| 14√3 | ||
a w odpowiedziach jest ze R = | ||
| 3 |
| 5√3 | 3√5 | |||
Najpierw psizesz ze sinα wynosi | a później przy sinusach wstawiasz | |||
| 14 | 14 |
| 70√75 | 14√25 * 3 | 14 * 5 * √3 | 14√3 | ||||
= | = | = | |||||
| 75 | 15 | 15 | 3 |
| 10 | 140 | |||||||||
2R = | = | |||||||||
| 5√3 |
| 140 | 140√3 | 14√3 | ||||
R = | = | = | ||||
| 10√3 | 30 | 3 |