7117 ***: na sześciokącie foremnym opisano okrag i w ten sam sześciokat wpisano okrag. Pole powstałego pierścienia kołowego jest równe 2πr .Oblicz pole tego szesciokąta dzieki

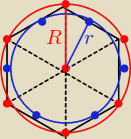
Eta: a −− długość boku sześciokąta foremnego R−− długość promienia okręgu opisanego więc R= a

	a√3
r −− dł. promienia okregu wpisanego, więc r= hΔrównoboczn.=
	2

P_pierścienia = P_k ( czerwonego) − P_k( niebieskiego) zatem Ppierścienia)= πa² − π(^a√3₂)²= πa² − ³₄πa² = ¹₄πa² więc : ¹₄πa² = 2πr => a² = 8r to:

	a2√3
Psześciokąta = 6*PΔrównoboczn.= 6*		= 32a2√3
	4

zatem po podstawieniu za a²= 8r mamy: P_{sześciokąta}= ³₂*8r*√3 = 12√3*r [j²