planimetria Kipic: Przekatna trapezu rownoramiennego ABCD tworzy z dłuzsza podstawaAB kat α , a z ramieniem AD kat β . Wyznacz stosunek pola trojkata ACD do pola trojkata ABC. Prosze o pomoc bo niemam pojecia jak to liczyc czy z twierdzenia sinusow czy cosinusow

	tg(α+β)−tgα
Kompletnie jestem bezradny bo w odpowiedziach wychodzi
	tg(α+β)+tg

Prosze o rozwiazanie lub chociaz o jakies wskazowki co jak po kolei liczyc z góry serdecznie dziękuje

Eta: Po rozwiązaniu ... też mam taką odpowiedź

Eta:

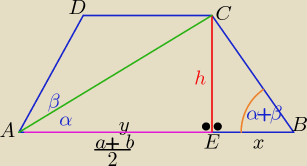
	h2		h
P(tr)= y*h =		bo y=
	tgα		tgα

	x+y		h
P(ΔEBC)=		*h , x=
	2		tg(α+β)

	h2		1		1		h2		tg(α+β)+tgα
P(ΔEBC)=		*(		+		)=		*
	2		tg(α+β)		tgα		2		tgα*tg(α+β)

P(ΔACD)= P(tr)−P(ΔEBC) =...... Myślę,że już sam dokończysz

Eta: jak leci?

Eta:

Albi:

	h2
P(tr)=y*h=		too jest pole trojkata AEC?
	tga

Kipic:

	h
z rysunku wynika ze y * h jest to wzor na obliczenie pola trapezu a że wiadomo ze y =
	tgα

to poproatu piszemy

	h2
P=
	tgα

Albi: aha no ok kminie bo teraz myslelm . bo na trapez do (a+b)/2 *h a y=(a+b)/2 ok git ^^

Albi: hmm a tam nie gdzies x+y/2 nie wyparowal h jak podstawiles? x i y? nie powinno byc h³?