Oblicz pole trójkąta oliwka552: W okrąg o promieniu 4 wpisano trójkąt w taki sposób, że środek okręgu leży na jednym boku trójkąta. Następnie w trójkąt wpisano okrąg o promieniu 0,5. oblicz pole tego trójkąta. wynik

	17
	4

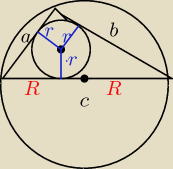Beti: r = 0,5 R = 4 c = 2R = 8 (a − 0,5) + (b − 0,5) = c a + b − 1 = 8 a + b = 9 a² + b² = c² rozwiązujemy powyższy układ równań: b = 9 − a a² + 81 − 18a + a² = 64 2a² − 18a + 17 = 0 Δ = 324 − 136 = 188 √Δ = 2√47

	18−2√47		9−√47
a1 =		=
	4		2

	9+√47
a2 =
	2

	9−√47		9+√47
b1 = 9 −		=
	2		2

	9+√47		9−√47
b2 = 9 −		=
	2		2

czyli:

	1		1		9+√47		9−√47		1(9+√47)(9−√47)
P =		ab =		*		*		=		=
	2		2		2		2		8

	81−47		34		17
=		=		=
	8		8		4