***: Siema W trojkącie ABC o bokach długości 5,6,7 poprowadzono wysokość prostopadłą do boku długości 6 .Wykaż że wysokość dzieli ten ten bok na odcinki których długości różnią się o 4 DZIĘKI

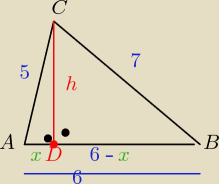
Eta: Witam 1/ sposób z tw. Pitagorasa w dla obydwu trójkatów otrzymasz: h² = 25 − x² i h² = 49 − ( 6 −x)² , x ∊( 0, 6) zatem: 49 − ( 6 −x)² = 25 +x² wyznaczamy "x" : 49 − x² +12x − x² = 25 − x² 12x =12 => x = 1 IADI=1 i IBDI = 5 2/ sposób : IBDI − IADI = 4 => 6 − x − x = 4 => 2x = 2 => x = 1 IADI = 1 i IDBI = 5 , zatem długości róznią się o 4

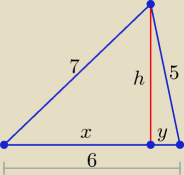
Bogdan: Przedstawię rozwiązanie podobne do rozwiązania 1, które pokazała Eta. x + y = 6 h² + x² = 49 h² + y² = 25 − −−−−−−−−−−−− x² − y² = 24 ⇒ (x − y)(x + y) = 24 ⇒ (x − y)*6 = 24 ⇒ x − y = 4

***: DZIĘKI