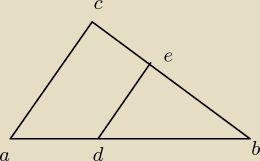
Grubo Planimetria Kipic: W trojkacie ABC o bokach długosci AB = 10 ,BC = 8 i AC = 6 poprowadzono prostą DE równolegla do boku AC Oblicz długosci odcinkow DB i EB jezeli prosta DE podzielila: a)obwód trójkąta ABC na dwie rowne czesci , b) trójkąt ABC na dwie figury o równych polach do podpunktu a to niewiem jak zrobić bo w jednym jest Liczona dlugosc AC a w drugim juz DE nie wiec wymieklem a na podpunkt b niemam pojecia Prosze o pomoc

Kipic: SRu

Kipic: dobra juz mam

Beti: Może tak: niech |DB| = x, |BE| = y a) L_ABC = 10+8+6 = 24 |AD|+|EC|+|CA| = x+y = 12 trójkąty ABC i DBE są podobne, więc:

	x		y
		=
	10		8

	5
x =		y
	4

powstaje więc układ równań do rozwiązania: x+y = 12

	5
x =		y
	4

	1
b) PADEC = PDBE =		PABC
	2

i ze wzoru Herona: P_ABC = √12*2*4*6 = √144*4 = 24 czyli: P_DBE = 12 z wł.: stosunek pól figur podobnych wynosi k² mamy:

PDBE		12		1		√2
	=		=		= k2 => k =
PABC		24		2		2

więc:

x		√2
	=		−−> x = ...
10		2

y		√2
	=		−−> y = ...
8		2

Beti: Spóżniłam się