Ewelinaaa: w trojkacie rownobocznym ABC na boku AB obrano tak punkt P ze jego odległość od boku AC jjest równa 3 a odległość od boku BC jest rowna 6 oblicz długosc odcinka CP (nie ma zadnego rysunku)

Eta:

	6
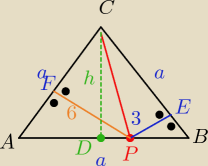
ΔAPF ~ ΔBPE w skali k=		= 2
	3

to: IAPI= ²₃*a i I PBI = ¹₃*a i IDPI= IAPI − IADI= ²₃a − ¹₂a = ¹₆a

	a√3
i h=
	2

należy wyznaczyć długość "a"

	a2√3
PΔABC=
	4

	a*6		a*3
PΔAPC =		= 3a [j2] i PΔPBC =		= 1,5a[j2]
	2		2

to P_ΔABC= 4,5a[j²} więc:

	a2√3
		= 4,5a => a = 6√3
	4

to : IDPI= ¹₆*6√3 = √3

	a√3		6√3*√3
i h=		=		= 9
	2		2

zatem: IPCI² = h² + IDPI² => IPCI² = 81 + 3 więc IPCI² = 84 to IPCI = 2√21 [j} Miłych snów o matematyce Bogdan pewnie poda jeszcze inną wersję

Ewelinaaa: dziekuje za zrobienie zadanka

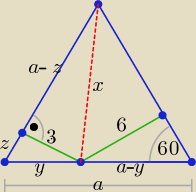
Bogdan: Dzień dobry. Podaję inny sposób rozwiązania.

3		3		√3		6
	= sin60o ⇒		=		⇒ y =		= 2√3
y		y		2		√3

6		6		√3
	= sin60o ⇒		=		⇒ a − 2√3 = 4√3 ⇒ a = 6√3
a − y		a − 2√3		2

z		√3
	= ctg60o ⇒ z = 3*		= √3
3		3

a − z = 6√3 − √3 = 5√3 x = √3² + (a − z)² = √9 + 75 = √84 = 2√21

Eta: