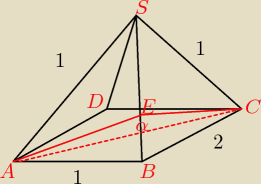
stereometria dla wybitnych Imosek: Mam bardzi trudne zadanie do rozwiazanie, ktore nauczyciel w liceum nie potrafii rozwiazac, takze prowsze o pomoc w rozwiazaniu: Podstawa ostroslupa ABCDS jest prostokąt ABCD, w ktorym |AB| =1 i |BC| = 2 Wszystkie krawedzie boczne tego ostroslupa maja dlugosc 1. Wyznacz wartosc funkcji trygonometryczenj kata miedzy dwiema sasiednimi scianami bocznymi tego ostroslupa. Nie wiem jak to narysować z tylu ksiazki mam odpowiedz, ale nie wiem dlaczego jest to tak narysowane.

PuRXUTM: c.d.n

Imosek: wlasnie nie tak nie jest.

Imosek: sorki tam u gory dlugosc druga jest rowna √2

Imosek: tak jes tz tylu

PuRXUTM:

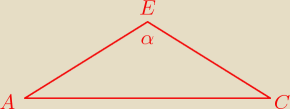
	√3
AE to wysokość trójkąta równobocznego ABS o boku 1 |AE|=		(poprzedni rysunek)
	2

EC to wysokość trójkąta równoramiennego BCS i wynosi ona.... Wychodzi mi z tego że to zadanie jest źle, może się nie znam ale w trójkącie BSC długości boków wynoszą 1,1,2 czyli to nie jest trójkąt.... czyli moim zdaniem źle zadanie ułożone ale mogę się mylić

PuRXUTM: |BC|=√2 ?

ziooom: tak

Imosek: tak

PW: PuRXUTM ma rację − jak może krawędź w podstawie mieć długość 2, a krawędzie boczne 1? Nie jest spełniony warunek trójkąta.

Imosek: No napisalem ze jednak maja √2

Imosek: no nikt nie wie?

dero2005: czy jest odpowieź do tego zadania?

PW: Kąt między dwiema płaszczyznami mierzy się przecinając je trzecią płaszczyzną − prostopadłą do krawędzi tych pierwszych. Płaszczyzna będzie prostopadła do krawędzi, jeżeli będzie wyznaczona przez dwie proste prostopadłe do tej krawędzi (twierdzenie o trzech prostopadłych). Musimy więc wygrać dowolny punkt P na krawędzi bocznej i skonstruować w tym punkcie dwie prostopadłe do tej krawędzi. Dobrze jet wybrać punkt P nie byle gdzie, ale tak, żeby prostopadłe leżały na ścianach w "dobrych miejscach". Bierzemy więc P taki, żeby jedna prostopadła dziabnęła wierzchołek w podstawie. Druga już nie będzie wedle naszego życzenia, tylko tam, gdzie musi żeby była prostopadła do krawędzi − stąd taki rysunek (ściany boczne nie są przystającymi trójkątami).

Imosek: mozesz to jakoss tak narysować zebym dobrze widzial o co gdzie ci jaki punkt chodzi?

Imosek:

PW: Dwie sąsiednie ściany to trójkąty równoramienne, ale jeden ma podstawę długości 1, a drugi długości √2. Wybierz taki punkt P, żeby prostopadła do ramienia w jednym z tych trójkątów trafiła w wierzchołek przy podstawie. Zobacz, gdzie trafi prostopadła poprowadzona z punktu P w drugim trójkącie. Masz przecież rysunek w książce − podałeś go wyżej.

Imosek: w srodek tej drugiej?

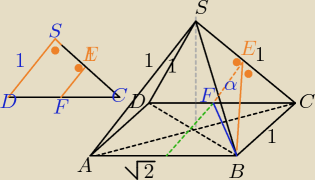
Mila: Jak pięknie tłumaczy PW, mamy: Prowadzimy prostopadłą z punktu B do SC, Punkt E jest środkiem SC, ΔBCS jest równoboczny. ΔDCS jest równoramienny (√2)²=1²+1²⇔2=2 ΔDCS jest równoramienny i prostokątny.

	√3
EB=
	2

	1
EF=		z tw. Talesa ( na bocznym rysunku)
	2

	1
FB2=(1)2+(		√2)2 z ΔBCF
	2

	3
FB2=
	2

3		1		√3		1	√3
	=(		)2+(		)2−2*			cosα w ΔBFE
2		2		2		2	2

3		1		3		√3
	=(		)+		−		cosα
2		4		4		2

	√3
cosα=−
	3

No, nie wiem, czy czegoś nie zgubiłam.

Imosek: wynik jest dobry...tylko teraz mam pytanie jak wyznaczyc w czyms takim kad dwuscienny skad mam wiedziec ze on akurat będzie w polowie tego drugiego boku? bo jak narysuje to w innej perspektywie to tak nie widac ze kat prosty tak bedzie na ten bok √2

Mila: Przeczytaj co napisałam o dwóch ścianach bocznych, Ramiona kąta, który jest miarą kata dwuściennego są prostopadłe do krawędzi SC. Wysokość z wierzchołka B do krawędzi SC to wysokość Δ równobocznego, kłopot z tym drugim ramieniem, musi być równoległe do SD, bo ΔDCS jest prostokątny, wyjaśnione na bocznym rysunku.

Mila: Imosek ?

Imosek: aha Mila dziękuję Ci bardzo

Mila: Pomogło?