trygonomatria natalia: Funkcja f dana jest wzorem f(x)=1+sin(−x) + cos(^π₂ +x). Wyznacz te wartości parametru m, dla których równanie f(x)=m ma dwa rozwiązania w przedziale <π,2π> Pomóżcie! :C

zombi: Nie wiem czy nie naginam trochę zasad, ale cos(^π₂+x)=cos(^π₂−(−x)) wiemy, że cos(a−b)=cosacosb+sinasinb gdzie a=^π₂ b=(−x), czyli dalej cos(^π₂+x)=cos(^π₂−(−x))=cos(^π₂)cos(−x)+sin(^π₂)sin(−x)=0*c os(−x)+sin(−x)=sin(−x) stąd f(x)=1+sin(−x)+sin(−x)=2sin(−x)+1 narysowac i odczytać

vitek1980: wzór przekształcamy: sin(−x) = −sin(x) cos(pi/2 + x) = sin(x) f(x) = 1−sin(x)+sin(x) = 1 − funkcja stała czyli dla m = 1 równanie f(x)=m ma ∞ rozwiązań a dla m ≠ 1 wcale

zombi: Dobra nie patrz na mój post, jestem głupkiem

zombi: albo i nie http://www.wolframalpha.com/input/?i=f%28x%29%3D1%2Bsin%28%E2%88%92x%29+%2B+cos%28pi%2F2+%2Bx%29 Wolfram nie kłamie

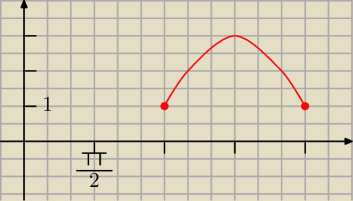
Saizou : f(x)=1+sin(−x)+cos(90+x)= 1−sinx+cos90cosx−sin90sinx= 1−sinx−0*cosx−1sinx= 1−2sinx i z wykresu widać że 2 rozwiązania ma dla m∊<1:3)

zombi:

vitek1980: racja, mój błąd