wartość funkcji Michalina:

	1
Znajdź największą i najmniejszą wartość funkcji f(x)=		dla x należącego do [0,2]
	1−x−x2

Chodzi mi głównie o to, czy po obliczeniu Xw dla równania w mianowniku muszę podstawiać do głównego wzoru funkcji, żeby ostatecznie uzyskać wartość Xw? czy po prostu Xw = {1}{2} i to jest koniec

aniabb: musisz wstawić do wzoru żeby uzyskać WARTOŚĆ czyli f(x_w) a poza tym jeszcze f(0) i f(2) i porównać która największa a która najmniejsza

Michalina: dziękuję

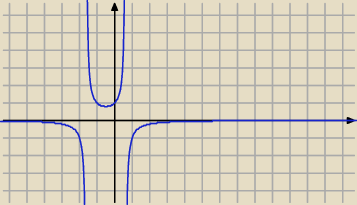
aniabb: tu jeszcze miejsca zerowe znajdź, bo się okazuje że się załapują w badany przedział, więc nie ma największej i najmniejszej, bo biegną w nieskończoności

aniabb: no i x_w = −1/2, więc jest poza zakresem, zatem nie trzeba go było uwzględniać

Artur_z_miasta_Neptuna: Aniu .... to co napisalas jest prawdą ... jezeli funkcja f(x) jest ciągła na badanym przedziale ... a tutaj ewidentnie nie jest (patrz wykres 12:46)

Artur_z_miasta_Neptuna: dlatego powinno się: 1) zbadać dziedzinę 2) jezeli jakiś punkt z badanego przedziału 'wypada' z dziedziny to sprawdzić granice jednostronne dla tego punktu 3) i te granice moga zaburzyć rozwiązanie w tym konkretnym przypadku −−− brak najmniejszej i największej wartości w badanym przedziale