Kilka upewnień KevyB: Hello, Mam po raz kolejny kilka prośb o pomoc, ale już coraz bliżej jestem opanowania całego materiału na poprawke. Pierwszy problem, a raczej zapytanie, tyczy się rozwiązywania nierówności i zaznaczenia zbioru rozwiązań na osi liczbowej. np takie coś:

	4−x		2x+2		5x−1
2x −		− 6 <		−
	3		2		6

pomnoze sobie całość przez sześć, i odrazu pytanie/ da sie tak? chce usunąć ułamki i doprowadzić je do formy całkowitej mam na myśli takie coś 12x − 8 − 2x − 36 < 6x + 6 − 5x−1 pamietam teraz coś że używało się form zdaniowych, ale nie jestem pewien czy to było przy tym, chodzi mi o znak v czyli "lub" to było do tego czy innego rodzaju? (układy równań np.) i mam wrazenie ze chyba sie gdzieś potknąłem d; −K

tim: Tzn tak, potknąłeś się. Choć samo mnożenie przez 6 jest ok, to już wynik po mnożeniu już nie. Mamy: 2x * 6 = 12x

	4 − x
−		* 6 = −2(4 − x) = −8 + 2x
	3

− 6 * 6 = −36

2x + 2
	* 6 = 3(2x + 2) = 6x + 6
2

	5x − 1
−		* 6 = −(5x − 1) = −5x + 1
	6

tim: Oczywiśćie można najpierw uiprościć: 2x + 2 / 2 = x + 1

Eta: Witam KevyB Z tego co pamiętam , obiecałeś się poprawić i pisać nawiasy ,a następnie zmieniać znaki przy opuszczaniu odpowiednich nawiasów , i co? widzę kardynalne błędy po pomnożeniu obydwu stron nierówności otrzymasz: 12x −2( 4 −x) −36 < 3( 2x +2) −(5x−1) opuszczajac nawiasy : 12x −8 +2x −36 < 6x +6 −5x +1

KevyB: troche niewyspany jestem d; ale zrobilem sobie kawy i zaraz bedzie ok. Sprobuje to zrobic teraz

Eta: powodzenia!

tim: Eto, mogłabyś?

KevyB: 13x < 51 | :13 x< 3.9230769231 bleh brzydki wynik, a czy dobry?

KevyB:

tim: 1. Nie zaokrąglamy

	51
2.		− dobry.
	13

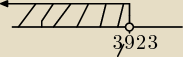
KevyB: to troche dziwnie takie cos by sie zaznaczylo na osi d; ale tak to dobrze narysowalem ? (otwarte kolko bo jest < a nie ≤ )

tim: Tak dobrze, ale musi być w ułamku.

KevyB: hm, przy takim np. przykładzie zaczynam za dużo próbować i mi sie kitra coś.

	3x−2		5		1
(		)2 − (x+1)2 <		(x−1)(x+1) − (4		)2
	2		4		2

KevyB: hm, przy takim np. przykładzie zaczynam za dużo próbować i mi sie kitra coś.

	3x−2		5		1
(		)2 − (x+1)2 <		(x−1)(x+1) − (4		)2
	2		4		2

KevyB: hm, przy takim np. przykładzie zaczynam za dużo próbować i mi sie kitra coś.

	3x−2		5		1
(		)2 − (x+1)2 <		(x−1)(x+1) − (4		)2
	2		4		2

tim: Wam też forum zamula? Najpierw rozbij wzory skróconego mnożenia, a ułamki właściwe zamień na niewłaściwe. Pokaż co zostanie.

KevyB: uojezu czego to sie 3 razy wyslalo o.0 fakt forum mi sie przez chwile nie ladowalo..

KevyB:

	3x−2		5		81
(		)2 − (x2 + 2x + 1) <		(x2 − 1) −
	2		4		4

Eta: Dokończę .... jestem "nocnym Markiem" mnożymy nierówność przez 4 (3x −2)² −4( ( x² +2x +1)< 5( x² −1) − 81 9x² −12x +4 −4x² −8x −4 < 5x² −5 −81 −20x < −86 /:( −20) x > 4,3 x€( 4,3 ; ∞)

KevyB: tam przypadkiem przy (3x − 2)² nie powinno byc 2 przed nawiasem?

KevyB: no nie moge rozkminic co sie stalo tam ze w nawiasie kwadratowym 2 poprostu zniknela a wartosci pozostaly te same, co to za operacja o.0

wsn: ta 2 jest w mianowniku w nawiasie i ją też obowiązuje kwadrat... więc jak ją podniesiesz do tego kwadratu ( w myślach) to z czwórką Ci się skróci i żadna 2 przed nawiasem nie zostanie, a 3x−2 pozostaje w nawiasie pod kwadratem.. przy dzieleniu czy mnożeniu może sobie to rozdzielić tak: było (3x−2 /2)² a możesz to zapisać: (3x−2)²/2² i masz (3x−2)²/4

KevyB:

	4
a czyli to tak jakbym odrazu nawias podniosl do kwadratu caly i potem przemnożył przez
	1

	9x2 − 12x + 4		4
i wtedy to jest takie		*		i to 4 z 4 znika i pozostaje 9x2 − 12x +
	4		1

4 , tak?

wsn: tak, tylko ten górny możesz zostawić w formie z kwadratem, żeby Ci się nie pomyliło przy przepisywaniu i rozpisać go po skróceniu, ale tak, o to chodzi. Skracasz te 4/1 z tą 2²