Zespolone Monika: Zaznaczyć na płaszczyźnie zespolonej zbiory punktów:

	π
arg(z+3)≥
	3

Monika: proszę o pomoc!

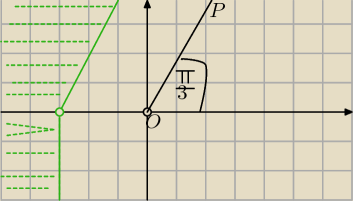Mila: Moniko, narysuję Ci zbiór

	π
arg(z+3)=
	3

	π
Na półprostej OP ( część prostej y=√3x ) leżą liczby które mają argument φ=
	3

arg(z+3)=arg[(x+3)+iy] Po przesunięciu półprostej o wektor [−3,0] otrzymamy pólprostą y=√3x+3√3i na niej leżą liczby takie, że

	π
arg(z+3)=
	3

Jeśli chodzi o nierówność, to mam wątpliwości, może masz coś w zeszycie z ćwiczeń, nie wiem jak ograniczyć od dołu, z prawej.

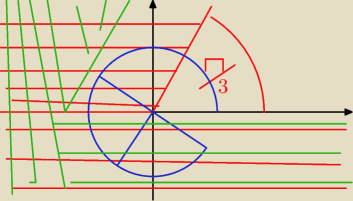Basia: to czerwone to wykres argz ≥ ^π₃ katy zaznaczone na niebiesko też są ≥ ^π₃ i teraz wystarczy to przesunąć o wektor [−3;0] algebraicznie to jest tak: φ≥^π₃ ⇔ tgφ≥√3 ∨ tgφ<0 ∨ φ=^π₂ ∨ φ=^3π₂ stąd mamy

y
	≥ √3
x+3

y ≥ √3x + 3√3 lub

y
	<0
x+3

y <0 i x>−3 lub y>0 i x<−3 lub x+3 = 0 ⇔ x= −3 a to jest to zielone