1.90. Trójkąt ostrokątny równoramienny ABC, (I∡BI = I∡CI), wpisano okrąg. Abdul: 1.90. Trójkąt ostrokątny równoramienny ABC, (I∡BI = I∡CI), wpisano okrąg. Nastepnie przez punkty B i C poprowadzono styczne do okręgu przecinające się w punkcie D. Miara kata CDB jest dwa razy mniejsza odmiary kąta przy podstawie trójkąta ABC. Oblicz miarę kąta BAC.

tim: Trójkąt wpisano W okrąg czy W trójkąt wpisano okrąg...

Abdul: wpisano w okrąg sory

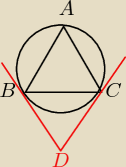
tim: Czy na pewno taka jest treść zadania (chodzi o kąty CDB oraz ABC)

Abdul: tak trzeba obliczyć kąt BAC

tim: Tzn chodzi mi o: "Miara kąta CDB jest dwa razy mniejsza od miary kąta przy podstawie (ABC lub ACB) w trójkącie ABC."

Abdul: tak

guuhh: αδδγβ∞∑∑∅