pomocy natalia: Rozwiąż nierówność 2cos(x+ ^π₂ ) ≥ − √2 dochodzę do x+^π₂ = −^√2₂ i czy ktoś mógły dalej pomóc?

natalia: * ≥

PW: Tak nie wolno myśleć, funkcja cosinus nie jest rosnąca!

	π		√2
Trzeba narysować wykres i wyciągnąć wnioski − dla jakich x cos(x+		)≥−
	2		2

	π
Dobrze jest najpierw zastosować wzór redukcyjny cos(x+		)=−sinx − łatwiej narysować.
	2

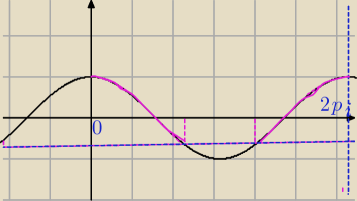Mila: Jeśli nie przekształcimy wzoru to tak:

	π		−√2
cos(x+		)≥
	2		2

	3		−√2		5π		−√2
cos		π=		lub cos(		)=
	4		2		4		2

Rysujemy wykres funkcji y=cosx i odczytujemy w przedziale <0,2π> dla jakich argumentów zachodzi nierówność:

	π		3		5		π
0+2kπ ≤x+		≤		π+2kπ lub		π+2kπ ≤x+		≤2π+2kπ
	2		4		4		2

	π				3		1
−		+2kπ≤x≤		π+2kπ lub		π +2kπ≤x≤2		π+2kπ
	2		4		4		2