Funkcje wymierne FlashCB:

	−4x − 6
Zbadaj liczbę rozwiązań równania |		| = m ze względu na wartość parametru m
	x + 1

(m∊R). Nie mam zielonego pojęcia, jak się za to zabrać, próbowałem kilkukrotnie, ale nic z tego Będę wdzięczny za wszelkie podpowiedzi i porady

FlashCB: Błagam, pomocy Zupełnie nie wiem, co z tym przykładem zrobić...

yeti:

	−2
Ja bym zrobil tak |		−4|=m
	x+1

Teraz rysujesz to co pod wartoscia bezwzgledna otrzymasz pewne odbicie i potem na podstawie rysunku odczytujesz ilosc rozwiazan

yeti: oczywiscie −1 nie mozesz podstawic za x z wiadomych wzgledow

FlashCB:

	−4x − 6		− 2
Hmm, a skąd z postaci: |		| wzięło się |		−4| ?
	x + 1		x + 1

yeti: spraowadz liczbe −4 do wspolnego mianownika

FlashCB: Mhm, dobra, stąd odczytuje przesunięcie [−1,−4], narysowałem wykres, lecz w jaki sposób można wyznaczyć liczbę rozwiązań ze względu na parametr m?

Dominik: przecinaj to wykres funkcji ktora narysowales prosta y = m. odpowiednio zapisuj dla jakiego m masz ile punktow przeciec.

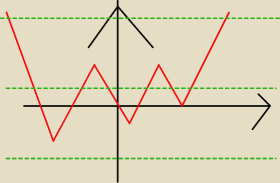
yeti: popatrz masz wykres jakis tam losowy Ten czerwony ta zielona prosta to wlasnie jest ten parametr m ( bo zauwaz ze m to przeciez wynik twojej funkcji bo ona rowna jest m zatem przesuwaz sobie w wyobrazni ten parametr m po osi Y czyli od −∞ do +∞ i otrzymasz takie wyniki ze np od −∞do 0 nie ma przeciez z wykresem zatem brak rozwiazan pozniej obczajasz skad do kad ma 4 przeciecia czyli 4 rozwiazania itd az oblecisz calą os Y

pigor: ... , najlepiej zrobić to przy pomocy wykresu funkcji lewej strony danego równania :

	−4x−6		−2(2x+3)
y= |		| i x+1≠0 ⇔ y= |		| i x≠−1, gdzie
	x+1		x+1

	2x+3		2x+2+1		2(x+1)+1		1
f(x)= 2*		= 2*		2*		= 2(2+		) , czyli
	x+1		x+1		x+1		x+1

	2
f(x)= 4+		− funkcja homograficzna , której wykres łatwo powstaje z hiperboli
	x+1

	2
y=		przez przesuniecie o wektor [−1,4] (o 1 w lewo i o 4 w górę), czyli punkt
	x

(−1,4), to punkt przecięcia się asymptot x=−1 i y=4 ; dalej ponieważ f(x)=0 ⇔ 2x+3=0 ⇔ x= −1,5 , to część hiperboli w przedziale <−1,5; −1) odbijasz symetrycznie względem osi OX i otrzymujesz wykres lewej strony twojego równania, z którego odczytujesz "przesuwając" prostą y=m równoległą do osi OX od dołu w górę liczbę punktów przecięcia się tej prostej z otrzymanym wykresem, czyli szukaną liczbę rozwiązań w zależności od m np. g(m) danego równania i tak : { 0 rozwiązań, gdy m< 0 ⇔ m∊(−∞;0) , g(m)= { 1 rozwiązanie, gdy m=0 lub m=4 ⇔ m∊{0,4} , { 2 rozwiązania, gdy 0< m<4 lub 4< m ⇔ m∊(0;4)U(4;+∞) i to tyle . ...

FlashCB: Chwilka, analizuje Twoje rozwiązanie @pigor i czy na początku, gdy wyciągasz 2 przed ułamek, to nie powinno być −2? I wtedy wektor q będzie −4, czyli asymptota będzie 4 w dół i wtedy odbijam część hiperboli z przedziału (−∞, −1,5> oraz hiperbolę z przedziału (−1, +∞), bo jest pod osią OX, a fragment <−1,5 , −1) mam juz nad osia Ale dzięki temu wyjaśnieniu zrozumiałem całą istotę robienia tego typu zadań Prze ogromne dzięki dla wszystkich, którzy próbowali mi to wyjaśnić, dzięki

pigor: ... , nie bo |−2|= 2

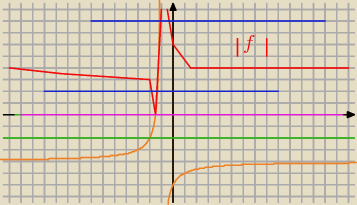
Aga1.: Dla m=4 , brak rozwiązań, czy źle widzę?

FlashCB: Dla m=4 jest jedno rozwiązanie − to w przedziale <−1,5, −1)

yeti: jeszcze to meczysz

pigor: ,,, tak, także dla m=4 jest jedno rozwiązanie, mimo, że y=4 jest asymptotą poziomą w x → ±∞ .