5.13 Naszkicuj wykres funkcji
wojtek: Rysowanie wykresów funkcji Kiełbasy
a) f(x)=x
2−3|x|+2
b) f(x)=x*|x−4|
c) f(x)=|x
2−4|+3x
Proszę chociaż o pierwszy przykład, resztę tylko jak komuś się chce.
W odpowiedziach jest napisane, że wykres x
2−3x+2 trzeba odbić względem osi OX, czego
kompletnie nie rozumiem dlaczego tak. Bardziej by mi pasowało odbicie względem OY i wykresy
"scalałyby" się w punkcie (0,2). Wytłumacz ktoś, a najlepiej narysuj.

3 mar 14:27
Artur_z_miasta_Neptuna:
a)
jeżeli x≥0 to:
f(x) = x2−3*(+x) + 2 ... rozwiązujesz
jeżeli x<0 to:
f(x) = x2−3*(−x) + 2 ... rozwiązujesz
3 mar 14:29
Artur_z_miasta_Neptuna:
a może to jest |x
2−3x+2|

wtedy odpowiedź byłaby prawidłowa
3 mar 14:30
Kejt: pamiętaj, że
|x|≥0
więc funkcja, nie może przyjąć wartości mniejszych od zera..
dlatego odbijasz ją względem OX.
narysuję Ci prosty przykład..
3 mar 14:30
wojtek: @Artur Nie, dobrze napisałem, tylko x przy trójce jest z wartością bezwzględną.
3 mar 14:33
Kejt: dobra, nieważne..
ja mam chyba dzisiaj jakiś problem z czytaniem ze zrozumieniem.
chyba za dużo farb olejnych się nawdychałam

3 mar 14:33
wojtek: To jak będzie? Coś takiego? Czy po lewej stronie jeszcze trzeba wartości ujemne na górę odbić?
http://i50.tinypic.com/2wdulc9.jpg
Sorry za link, nie umiem tutaj rysować

3 mar 14:46
Mila:
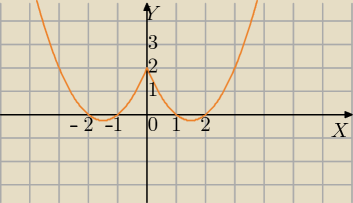
Odnośnie (a) pomyłka w druku,
Rysujemy g(x)=x
2−3x+2 dla x≥0 i odbijamy symetrycznie względem osi OY, ponieważ
f(x)=x
2−3|x|+2 przyjmuje te same wartości dla przeciwnych argumentów
np.f(2)=f(−2)=0
3 mar 14:56
wojtek: No, o to mi chodziło. Dzięki Mila. Wczoraj też miałem zagwozdkę nad pewnym zadaniem (ze zbioru
Kiełbasy). Sprawdzam je w necie, a tu ludzie piszą, że musi być błąd w treści.
3 mar 15:00
Dominik: w zbiorze A. Kielbasy jest sporo bledow.

3 mar 15:00
Mila:
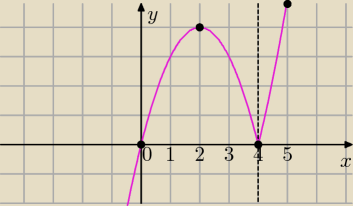
b) rozpisujemy na dwa przypadki
f(x)=x*|x−4|
b.1) x−4≥0⇔x≥4⇔|x−4|=x−4
f(x)=x(x−4)szkicujemy wykres tej funkcji dla x≥4
(x
1=0∉D ) x
2=4
f(5)=5
b.2) x<4
|x−4=−x+4
f(x)=x*(−x+4)
f(x)=−x
2+4x
x
w=2, y
w=4
x
1=0,( x
2=4∉D)
3 mar 15:07
Mila:
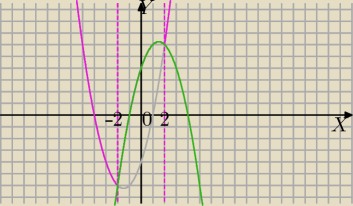
c)
f(x)=|x
2−4|+3x
c.1) x
2−4≥0⇔x≥2 lub x≤−2⇔
|x
2−4|=x
2−4
f(x)= x
2−4+3x
f(x)=x
2+3x−4 szkicuje cały wykres (popielaty), na różowo będzie część dla x∊(−
∞,−2>∪<2,
∞)
c.2) x∊(−2,2)
|x
2−4|=−x
2+4
f(x)=−x
2+3x+4 zielony, bierzesz pod uwagę tylko część dla x∊(−2,2)
Na następnym narysuję zbiorczo tylko
f(x)=|x
2−4|+3x
3 mar 15:22
Mila:
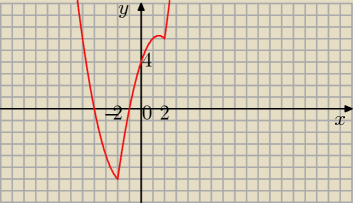
f(x)=|x
2−4|+3x
3 mar 15:24
wojtek: Dziękuję bardzo


3 mar 15:25
Mila: 
3 mar 16:13

 wtedy odpowiedź byłaby prawidłowa
wtedy odpowiedź byłaby prawidłowa


 Odnośnie (a) pomyłka w druku,
Rysujemy g(x)=x2−3x+2 dla x≥0 i odbijamy symetrycznie względem osi OY, ponieważ
f(x)=x2−3|x|+2 przyjmuje te same wartości dla przeciwnych argumentów
np.f(2)=f(−2)=0
Odnośnie (a) pomyłka w druku,
Rysujemy g(x)=x2−3x+2 dla x≥0 i odbijamy symetrycznie względem osi OY, ponieważ
f(x)=x2−3|x|+2 przyjmuje te same wartości dla przeciwnych argumentów
np.f(2)=f(−2)=0

 b) rozpisujemy na dwa przypadki
f(x)=x*|x−4|
b.1) x−4≥0⇔x≥4⇔|x−4|=x−4
f(x)=x(x−4)szkicujemy wykres tej funkcji dla x≥4
(x1=0∉D ) x2=4
f(5)=5
b.2) x<4
|x−4=−x+4
f(x)=x*(−x+4)
f(x)=−x2+4x
xw=2, yw=4
x1=0,( x2=4∉D)
b) rozpisujemy na dwa przypadki
f(x)=x*|x−4|
b.1) x−4≥0⇔x≥4⇔|x−4|=x−4
f(x)=x(x−4)szkicujemy wykres tej funkcji dla x≥4
(x1=0∉D ) x2=4
f(5)=5
b.2) x<4
|x−4=−x+4
f(x)=x*(−x+4)
f(x)=−x2+4x
xw=2, yw=4
x1=0,( x2=4∉D)
 c)
f(x)=|x2−4|+3x
c.1) x2−4≥0⇔x≥2 lub x≤−2⇔
|x2−4|=x2−4
f(x)= x2−4+3x
f(x)=x2+3x−4 szkicuje cały wykres (popielaty), na różowo będzie część dla x∊(−∞,−2>∪<2,∞)
c.2) x∊(−2,2)
|x2−4|=−x2+4
f(x)=−x2+3x+4 zielony, bierzesz pod uwagę tylko część dla x∊(−2,2)
Na następnym narysuję zbiorczo tylko
f(x)=|x2−4|+3x
c)
f(x)=|x2−4|+3x
c.1) x2−4≥0⇔x≥2 lub x≤−2⇔
|x2−4|=x2−4
f(x)= x2−4+3x
f(x)=x2+3x−4 szkicuje cały wykres (popielaty), na różowo będzie część dla x∊(−∞,−2>∪<2,∞)
c.2) x∊(−2,2)
|x2−4|=−x2+4
f(x)=−x2+3x+4 zielony, bierzesz pod uwagę tylko część dla x∊(−2,2)
Na następnym narysuję zbiorczo tylko
f(x)=|x2−4|+3x
 f(x)=|x2−4|+3x
f(x)=|x2−4|+3x


