Podaj wszystkie liczby całkowite Majka : Podaj wszystkie liczby całkowite, dla których zachodzi nierówność : a) x² ≤ 16 b) 16 + x² > 8x Wytłumaczy mi ktoś jak to obliczyć ?

Kejt: choćby tak: x²−16=0 (x+4)(x−4)=0 x=4 v x=−4 i do tego rysunek...zaraz wrzucę..

krystek: x²−4²≤0 ⇔(x+4)(x−4)≤0 naszkicuj wykres i podaj odpowiedź

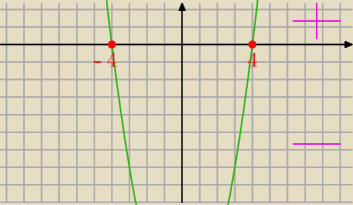
Kejt: i teraz sprawdzasz kiedy funkcja ≤0 czyli patrzysz na część funkcji pod osią OX: x∊<−4;4> i przedziały domknięte, bo może być równa zero.

krystek: Kejt tylko całkowite ma wybrać.

Kejt: w przykładzie drugim policz miejsca zerowe z delty, podaj pierwiastki i zrób rysunek(nie jakiś super dokładny, tylko poglądowy, jak mój) na nim zaznaczasz miejsca zerowe i odczytujesz rozwiązanie. jakby co to pytaj

Kejt: no to sobie wybierze..ma przedział.

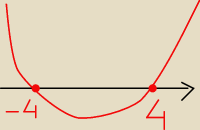
Majka : Mogę to tak narysować ?

Kejt: jasne, że tak teraz wypisz liczby całkowite.

Majka : −4, −3, −2, −1, 0, 1, 2, 3, 4 Dzięki wielkie

Kejt: nie ma sprawy jak wstawisz tutaj rozwiązanie tego drugiego...to mogę sprawdzić

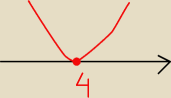
Majka : 16 + x² − 8x ≤ 0 x² − 8x +16 = 0 Δ= 64−64 = 0 x₀ = 4 czyli, x e 4

Kejt: dlaczego zmieniłaś znak nierówności?

Majka : Haha, w sumie nie wiem, czyli ciągle muszę, że ≤ ?

Kejt: podałaś w zadaniu, że jest >0 a tu nagle zmieniasz na ≤0 czyli liczysz coś zupełnie odwrotnego. nie chodzi mi o zamianę tego później na znak równości, kiedy liczysz sobie miejsca zerowe..to jest ok.

Majka : A no faktycznie, w treści miało być 16 + x² ≤ 8x , pomyliłam..

Kejt: a..okej. to jest dobrze..