Oblicz długość promienia okręgu
oliwka552:
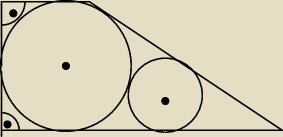
W trapez prostokątny wpisano okrąg, a następnie jeszcze jeden okrąg styczny do dwóch boków tego
trapezu. oblicz długość promienia mniejszego okręgu, jeśli dolna podstawa wynosi 28, krótsze
ramię 24, dłuższe ramię 25 i górna podstawa 21.
Janek191:
Niech ABCD będzie danym trapezem prostokątnym.
a = AB = 28
h = AD = 24
c = BC = 25
b = CD = 21
R − promień większego okręgu
r − promień mniejszego okręgu
R = 0,5 h = 12
O − środek większego okręgu
O
1 − środek mniejszego okręgu
K − punkt styczności większego okręgu z dolną podstawą trapezu
L − punkt styczności większego okręgu z dłuższym ramieniem trapezu
Mamy
AK = R = 12
więc
BK = 28 − 12 = 16
zatem
BL = 16
OK = OL = 12
Z tw. Pitagorasa mamy
OB
2 = 16
2 + 12
2 = 256 + 144 = 400
więc
OB = 20
S − punkt styczności obu okręgów
OS = R = 12 więc SB = 20 − 12 = 8
K
1 i L
1 − punkty styczności mniejszego okręgu z dolną podstawą trapezu
i jego dłuższym ramieniem
Mamy
KK
12 + ( R − r)
2 = OO
12
więc
KK
12 + ( 12 − r)
2 = ( 12 + r)
2
KK
12 + 144 − 24 r + r
2 = 144 + 24 r + r
2
KK
12 = 48 r
============
12* KK
1 = 16*( 12 − r) / : 12
zatem
| 16 | | 9 | |
| *( 12 − r)2 = 48 r / * |
| |
| 9 | | 16 | |
( 12 − r)
2 = 27 r
144 − 24 r + r
2 = 27 r
r
2 − 51 r + 144 = 0
−−−−−−−−−−−−−−−−−
Δ = ( − 51)
2 − 4*1*144 = 2 601 − 576 = 2 025
√Δ = 45
r = ( 51 − 45)/2 = 3
Odp. r = 3
=======================
 W trapez prostokątny wpisano okrąg, a następnie jeszcze jeden okrąg styczny do dwóch boków tego
trapezu. oblicz długość promienia mniejszego okręgu, jeśli dolna podstawa wynosi 28, krótsze
ramię 24, dłuższe ramię 25 i górna podstawa 21.
W trapez prostokątny wpisano okrąg, a następnie jeszcze jeden okrąg styczny do dwóch boków tego
trapezu. oblicz długość promienia mniejszego okręgu, jeśli dolna podstawa wynosi 28, krótsze
ramię 24, dłuższe ramię 25 i górna podstawa 21.
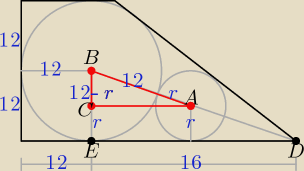 Niektóre dane liczbowe podane w treści zadania są zbędne.
|BD| = √122 + 162 = 20
Niektóre dane liczbowe podane w treści zadania są zbędne.
|BD| = √122 + 162 = 20