sss yeti: Siemka prosze pilnie o pomoc Narysuj w układzie współrzędnych zbiór punktów, których współrzędne spełniają równanie: x−|x|=y+|y| jak ten rysunek bedzie wygladal narysuje ktos

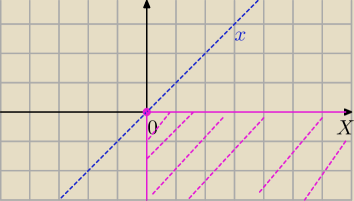
PW: Dlaczego "pilnie" − studiujesz w nocnym technikum? Trzeba pokombinować zanim sie narysuje. Dla x≥0 jest |x|=x, a więc lewa strona jest zerem, mamy zatem równanie 0 = y+|y| Oznacza to, że musi być |y|=−y, czyli y<0. Część rozwiązania już mamy: dla x≥0 są to y<0 − takie pary pijacy nazywają "czwarta ćwiartka". Pomyśl co będzie dla x<0 − trochę to trudniejsze, ale myślenie takie samo − co będzie dla y≥0, a co dla y<0.

yeti: pilnie poniewaz irytuje mnie juz to zadanie w odpowiedziach jest mowa tylko o rysunku dla cwiartki 4 tak jak ty to napisales ale przeciez dla cwiartki 2 mam x=y bo x<0 i Y>0 zatem otrzymamy x=y wiec powinna byc chyba narysowana prosta pod katem 45 stopni w drugiej cwiartce. Generalnie wiem mniej wiecej o co biega zalezy mi tylko na rysunku prawidlowym dla tego zadania dlatego prosilbym o narysowanie tego zbioru thx

Mila: x−|x|=y+|y| 1) rozważam sytuację, gdy y≥0 Punkty leżące w I i II ćwiartce 2y=x−|x|

	1
y=		(x−|x|)
	2

dwa przypadki: 1.1 x≥0 I ćwiartka

	1
y=		(x−x)=0 ⇔x≥0 i y=0 półprosta OX
	2

1.2 x<0 II ćwiartka

	1
y=		(x+x)⇔y=x wykres nie przechodzi przez II ćwiartkę
	2

2) y<0 III i IV ćwiartka x−|x|=y+|y| x−|x|=y−y x−|x|=0 2.1 x≥0 IV ćwiartka x−x=0 dla każdego x wszystkie punkty IV ćwiartki 2.2 x<0 x+x=0 2x=0 ⇔x=0∉D

PW: Zakładamy, że x<0. Równanie przyjmuje postać 2x = y+|y|, x<0 Dla y≥0 mamy więc 2x=2y, x<0 − to równanie nie ma rozwiązania (lewa strona ujemna, prawa nieujemna). a dla y<0 2x=0. x>0 − też rozwiązania nie ma. Pozostaje się upić ćwiartką (dokładnie − razem z półosiami), w moim rozwiązaniu z 22:36 można poprawić: |y|=−y, czyli y≤0 (w ten sposób nie zginą punkty (x,0) dla x≥0).

yeti: dzieki juz kumam