stereometria pic: Dany jest ostrosłup prawidłowy trójkątny. Odległość wierzchołka podstawy ostrosłupa od rozłączonej z nią krawędzi bocznej jest równa d. Kąt przy wierzchołku ostrosłupa ma miarę α. Wyznacz objętość ostrosłupa. http://wstaw.org/m/2013/03/02/zad3.png Znów mam problem z sporządzeniem rysunku. gdzie zaznaczyć tą odległość d i kąt alfa? Proszę o pomoc. Pozdrawiam

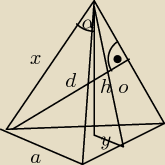
Jony: d/x=sinα x=dsinα ponieważ wysokość w trójkącie równoramiennym jest dwusieczną kąta to (a/2)/x=sin(α/2) z porównania pól 1/2*a*o=1/2*x²*sinα o=(x² sinα)/a y=a√3/6 h=√o²−y² dalej wystarczy podstawić do ostatecznego wzoru i mamy V= ((2*d*sinα*sin(α/2))²*√3*√[(dsin²α)/2sin(α/2)]² − [2*d*sinα*sin(α/2)]²/12)/6