aaa
yeti: Wyznacz równania prostych przechodzących przez punktP(−1,2) i stycznych do okręgu o równaniu
(x−3)
2+y
2=9.
Mam mega problem bo nie rozumiem calkowicie o co w tym zadaniu tak naprawde chodzi bo niby
wynik jakis jest ale przeciez punkt P lezy w SRODKU OKREGU wiec jakim cudem prosta moze
przechodzic przez ten punkt i jednoczexnie byc styczną do opkregu >>


?
2 mar 19:44
sushi_ gg6397228:
ciekawe jakim cudem masz punkt P w środku okręgu?
2 mar 19:52
Skipper:
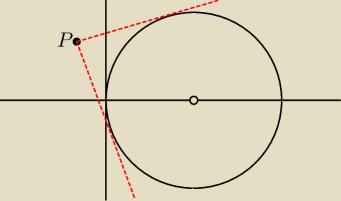

?
2 mar 19:56
yeti: kurde faktycznie, chyba na dzisiaj dam juz sobie spokoj z ta matematyką bo myle juz osie xd
byle tylko na maturze tak sie nie wpierdolic na mine xd dzieki stary

mimo wszystko mi
pomogles

2 mar 19:57
yeti: a mozecie do mojego wczesniejszego postu zagladnac gdzie pytalem czy dobrze narysowalem zbior
punktow
2 mar 19:58
nicoll: S(a,b)
S(3,0)
r=3
r=d
2=−a+b
b=2+a
y=−a+2+a
y−2=0
3=|0+0 −2|/ √1
3=|−2|/1
2 mar 19:58
Trivial:
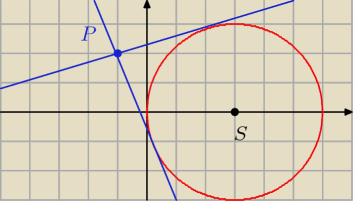
2 mar 20:00
Trivial: Eh, za późno.

2 mar 20:01

 ?
?

 ?
?
 mimo wszystko mi
pomogles
mimo wszystko mi
pomogles 

